
2.排列数的定义,排列数的计算公式
 或
或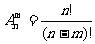 (其中m≤n m,nÎZ)
(其中m≤n m,nÎZ)
1.排列的定义,理解排列定义需要注意的几点问题;
例8. 已知函数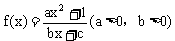 是奇函数,当x>0时,f(x)有最小值2,其中
是奇函数,当x>0时,f(x)有最小值2,其中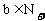 ,且
,且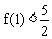
(1)试求f(x)的解析式;
(2)问函数f(x)的图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由。
解:知函数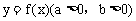 是奇函数,
是奇函数,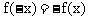 ,则c=0
,则c=0
由于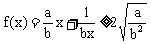 ,所以
,所以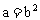 ,又
,又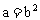 ,又
,又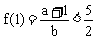 ,于是
,于是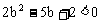
解得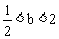 ,又
,又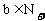
所以b=1,a=1
所以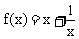
(2)设点(x0,y0)存在关于点(1,0)对称点(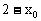 ,y0),此两点均在函数
,y0),此两点均在函数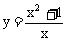 的图象上,则
的图象上,则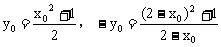
联立以上两式得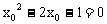 ,即
,即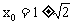 ,从而,当
,从而,当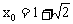 时,得
时,得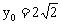 ;当
;当 时,得
时,得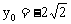
即存在点(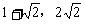 ),(
),(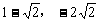 )关于点(1,0)对称。
)关于点(1,0)对称。
湖南省永州市第一中学(425006)
例7. 若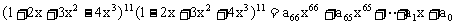 ,求
,求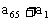 的值。
的值。
解:设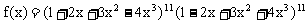 ,则f(x)是偶函数
,则f(x)是偶函数
则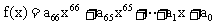 的奇数次方的系数
的奇数次方的系数
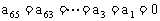
则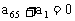
例5. 解不等式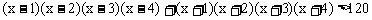
解:设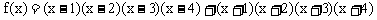 ,因
,因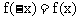 ,则f(x)是偶函数,即f(x)的奇数次方为0,可设
,则f(x)是偶函数,即f(x)的奇数次方为0,可设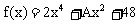 ,以x=1代入,得
,以x=1代入,得
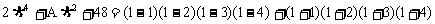
解得A=70,即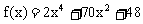 ,原不等式可化为:
,原不等式可化为:
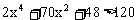
即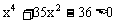
即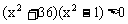
因而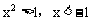 或x>1
或x>1
例6. (2004年上海卷)设奇函数f(x)的定义域是[-5,5]。当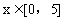 时,f(x)的图象如图1,则不等式f(x)<0的解是______________。
时,f(x)的图象如图1,则不等式f(x)<0的解是______________。
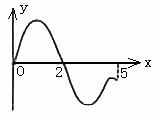
图1
解:根据奇函数图象关于原点成中心对称的性质,画出函数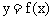 在区间[-5,5]上的图象如图2,易知不等式
在区间[-5,5]上的图象如图2,易知不等式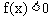 的解是
的解是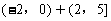 。
。
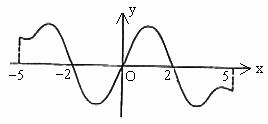
图2
例3. 设f(x)是定义在R上的奇函数,当x>0时,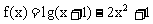 。试求此函数的解析式。
。试求此函数的解析式。
解:(1)当x=0时,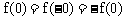 ,于是
,于是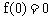 ;
;
(2)当x<0时,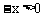 ,则
,则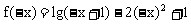 ,由于f(x)是定义在R上的奇函数,则
,由于f(x)是定义在R上的奇函数,则
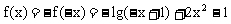
此函数的解析式为

例4. 设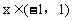 ,f(x)是奇函数,g(x)是偶函数,
,f(x)是奇函数,g(x)是偶函数,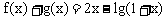 ,求f(x)的表示式。
,求f(x)的表示式。
解:f(x)是奇函数,有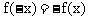 ;g(x)是偶函数,有
;g(x)是偶函数,有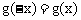 ,则
,则
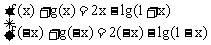
即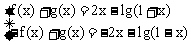
两式相减得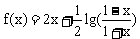
例3. 设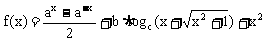 (其中a,b,c为常数),且
(其中a,b,c为常数),且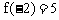 ,试求f(2)的值。
,试求f(2)的值。
解:设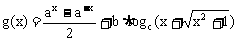 ,易证g(x)是奇函数,故
,易证g(x)是奇函数,故
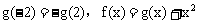
于是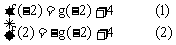
两式相加得: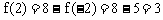 ,即
,即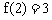
例1. 判定函数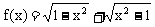 的奇偶性。
的奇偶性。
解:函数的定义域满足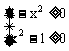 ,即为
,即为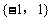 ,函数的图象表示两个点:(-1,0),(1,0)。其图象既关于原点对称,又关于y轴对称。从而函数f(x)既是奇函数又是偶函数。
,函数的图象表示两个点:(-1,0),(1,0)。其图象既关于原点对称,又关于y轴对称。从而函数f(x)既是奇函数又是偶函数。
8. 是定义在R上的偶函数,其图像关于直线
是定义在R上的偶函数,其图像关于直线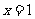 对称,
对称,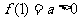 ,且对任意的
,且对任意的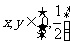
都有 .
.
(1)求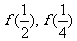 ;(2)证明:
;(2)证明: 是周期函数 .
是周期函数 .
(3)记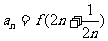 ,求
,求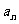 的通项公式.
的通项公式.
7.已知函数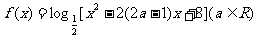
(1)若使函数f(x)在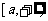 上为减函数,求a的取值范围;
上为减函数,求a的取值范围;
(2)若关于x的方程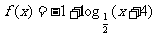 有且仅有一解,求a的取值范围.
有且仅有一解,求a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com