
学生练习:P122练习 1、2、3
3.例一 (P120 例一):用公式1求
2.推导公式2
用上述公式要求 必须具备三个条件:
必须具备三个条件:
但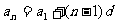 代入公式1即得:
代入公式1即得: 
此公式要求 必须具备三个条件:
必须具备三个条件: (有时比较有用)
(有时比较有用)
总之:两个公式都表明要求 必须已知
必须已知 中三个
中三个
1.证明公式1:
证明:
 ①
①
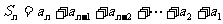 ②
②
①+②:
∵
∴ 由此得:
由此得:
从而我们可以验证高斯十岁时计算上述问题的正确性。
1+2+3+…+100的故事
故事结束:归结为 1.这是求等差数列1,2,3,…,100前100项和
2.高斯的解法是:前100项和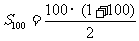
即
2.基本的解题方法:
⑴ 有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优限法);
⑵ 某些元素要求必须相邻时,可以先将这些元素看作一个元素,与其他元素排列后,再考虑相邻元素的内部排列,这种方法称为“捆绑法”;
⑶ 某些元素不相邻排列时,可以先排其他元素,再将这些不相邻元素插入空挡,这种方法称为“插空法”;
⑷ 在处理排列问题时,一般可采用直接和间接两种思维形式,从而寻求有效的解题途径,这是学好排列问题的根基.
1.对有约束条件的排列问题,应注意如下类型:
⑴某些元素不能在或必须排列在某一位置;
⑵某些元素要求连排(即必须相邻);
⑶某些元素要求分离(即不能相邻);
例1:⑴ 7位同学站成一排,共有多少种不同的排法?
解:问题可以看作:7个元素的全排列-- =5040
=5040
⑵ 7位同学站成两排(前3后4),共有多少种不同的排法?
解:根据分步计数原理:7×6×5×4×3×2×1=7!=5040
⑶ 7位同学站成一排,其中甲站在中间的位置,共有多少种不同的排法?
解:问题可以看作:余下的6个元素的全排列-- =720
=720
⑷ 7位同学站成一排,甲、乙只能站在两端的排法共有多少种?
解:根据分步计数原理:第一步 甲、乙站在两端有 种;第二步 余下的5名同学进行全排列有
种;第二步 余下的5名同学进行全排列有 种 则共有
种 则共有
 =240种排列方法
=240种排列方法
⑸ 7位同学站成一排,甲、乙不能站在排头和排尾的排法共有多少种?
解法一(直接法):第一步 从(除去甲、乙)其余的5位同学中选2位同学站在排头和排尾有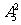 种方法;第二步 从余下的5位同学中选5位进行排列(全排列)有
种方法;第二步 从余下的5位同学中选5位进行排列(全排列)有 种方法 所以一共有
种方法 所以一共有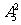
 =2400种排列方法.
=2400种排列方法.
解法二:(排除法)若甲站在排头有 种方法;若乙站在排尾有
种方法;若乙站在排尾有 种方法;若甲站在排头且乙站在排尾则有
种方法;若甲站在排头且乙站在排尾则有 种方法.所以甲不能站在排头,乙不能排在排尾的排法共有
种方法.所以甲不能站在排头,乙不能排在排尾的排法共有 -
- +
+ =2400种.
=2400种.
小结一:对于“在”与“不在”的问题,常常使用“直接法”或“排除法”,对某些特殊元素可以优先考虑.
例2 : 7位同学站成一排.
⑴甲、乙两同学必须相邻的排法共有多少种?
解:先将甲、乙两位同学“捆绑”在一起看成一个元素与其余的5个元素(同学)一起进行全排列有 种方法;再将甲、乙两个同学“松绑”进行排列有
种方法;再将甲、乙两个同学“松绑”进行排列有 种方法.所以这样的排法一共有
种方法.所以这样的排法一共有
 =1440种.
=1440种.
⑵甲、乙和丙三个同学都相邻的排法共有多少种?
解:方法同上,一共有
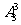 =720种.
=720种.
⑶甲、乙两同学必须相邻,而且丙不能站在排头和排尾的排法有多少种?
解法一:将甲、乙两同学“捆绑”在一起看成一个元素,此时一共有6个元素,因为丙不能站在排头和排尾,所以可以从其余的5个元素中选取2个元素放在排头和排尾,有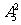 种方法;将剩下的4个元素进行全排列有
种方法;将剩下的4个元素进行全排列有 种方法;最后将甲、乙两个同学“松绑”进行排列有
种方法;最后将甲、乙两个同学“松绑”进行排列有 种方法.所以这样的排法一共有
种方法.所以这样的排法一共有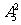

 =960种方法.
=960种方法.
解法二:将甲、乙两同学“捆绑”在一起看成一个元素,此时一共有6个元素,
若丙站在排头或排尾有2 种方法,所以丙不能站在排头和排尾的排法有
种方法,所以丙不能站在排头和排尾的排法有 种方法.
种方法.
解法三:将甲、乙两同学“捆绑”在一起看成一个元素,此时一共有6个元素,因为丙不能站在排头和排尾,所以可以从其余的四个位置选择共有 种方法,
种方法,
再将其余的5个元素进行全排列共有 种方法,最后将甲、乙两同学“松绑”,所以这样的排法一共有
种方法,最后将甲、乙两同学“松绑”,所以这样的排法一共有

 =960种方法.
=960种方法.
小结二:对于相邻问题,常用“捆绑法”(先捆后松).
例3: 7位同学站成一排.
⑴甲、乙两同学不能相邻的排法共有多少种?
解法一:(排除法)
解法二:(插空法)先将其余五个同学排好有 种方法,此时他们留下六个位置(就称为“空”吧),再将甲、乙同学分别插入这六个位置(空)有
种方法,此时他们留下六个位置(就称为“空”吧),再将甲、乙同学分别插入这六个位置(空)有 种方法,所以一共有
种方法,所以一共有 种方法.
种方法.
⑵甲、乙和丙三个同学都不能相邻的排法共有多少种?
解:先将其余四个同学排好有 种方法,此时他们留下五个“空”,再将甲、乙和丙三个同学分别插入这五个“空”有
种方法,此时他们留下五个“空”,再将甲、乙和丙三个同学分别插入这五个“空”有 种方法,所以一共有
种方法,所以一共有
 =1440种.
=1440种.
小结三:对于不相邻问题,常用“插空法”(特殊元素后考虑).
4.“分类”、“分步”思想在排列问题中的应用.
3.全排列、阶乘的意义;规定 0!=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com