
1.A.解析:由集合的运算法则.
21.(本小题满分14分)
已知曲线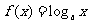 在
在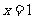 处的切线为
处的切线为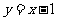 ,
,
(1)求实数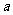 的值;
的值;
(2)若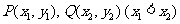 是曲线
是曲线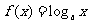 上的两点,且存在实数
上的两点,且存在实数 使得
使得
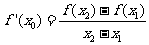 ,
,
证明: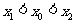 .
.
[答案及详细解析]
20.(本小题满分14分)
已知抛物线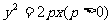 的焦点为
的焦点为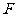 ,点
,点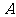 是抛物线上横坐标为4、且位于
是抛物线上横坐标为4、且位于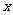 轴上方的点,点
轴上方的点,点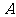 到抛物线准线的距离等于5,过
到抛物线准线的距离等于5,过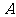 作
作 垂直
垂直 轴于点
轴于点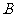 ,线段
,线段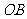 的中点为
的中点为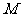 .
.
(1)求抛物线方程;
(2)过点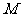 作
作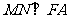 ,垂足为
,垂足为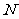 ,求点
,求点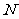 的坐标;
的坐标;
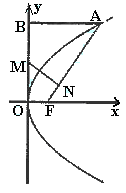 (3)以点
(3)以点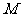 为圆心,
为圆心,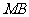 为半径作圆
为半径作圆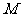 ,当
,当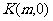 是
是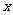 轴上一动点时,
轴上一动点时,
讨论直线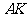 与圆
与圆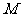 的位置关系.
的位置关系.
19.(本小题满分14分)
某公司2008年8月出口欧美的贸易额为2000万元,受金融危机的影响,从2008年9月开始,每月出口欧美的贸易额都比上一个月减少300万元,为了扭转这一局面,该公司充分挖掘内部潜力,加强品牌创新,形势出现转机,2009年1月出口欧美的贸易额比2008年12月增长25%,2009年2月出口欧美的贸易额比2009年1月也增长25%.
(1)该公司2008年12月出口欧美的贸易额是多少?
(2)假设2009年该公司出口欧美的贸易额都能保持25%的月增长率,问从哪个月开始该公司月出口欧
美的贸易额超过2000万元?(参考数据lg2=0.3010,lg3=0.4771)
18.(本小题满分14分)
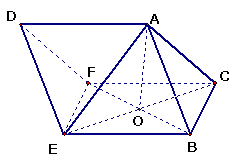
如图,在棱长均为2的三棱柱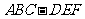 中,设侧面四边形
中,设侧面四边形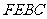 的两对角线相交于
的两对角线相交于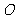 ,
,
 若
若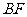 ⊥平面
⊥平面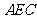 ,
,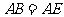 .
.
(1)
求证: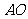 ⊥平面
⊥平面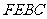 ;
;
(2)
求三棱锥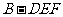 的体积.
的体积.
17.(本小题满分12分)
某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
|
日 期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
温差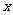 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
发芽数 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为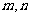 ,求事件“
,求事件“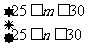 ”的概率;
”的概率;
(2)甲,乙两位同学都发现种子的发芽率与昼夜温差近似成线性关系,给出的拟合直线分别为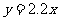 与
与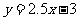 ,试利用“最小平方法(也称最小二乘法)的思想”,判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)的思想”,判断哪条直线拟合程度更好.
16.(本小题满分12分)
已知函数 一个周期的图象如图所示,
一个周期的图象如图所示,
(1)求函数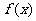 的表达式;
的表达式;
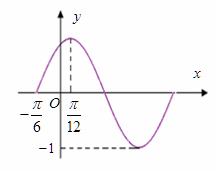 (2)若
(2)若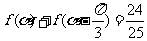 ,且
,且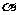 为
为 的一个内角,
的一个内角,
求 的值.
的值.
(二)选做题(13-15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)在直角坐标系中圆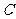 的参数方程为
的参数方程为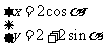 (
(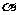 为参数),以原点
为参数),以原点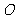 为极点,以
为极点,以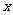 轴正半轴为极轴建立极坐标系,则圆
轴正半轴为极轴建立极坐标系,则圆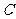 的极坐标方程为_____ ____.
的极坐标方程为_____ ____.
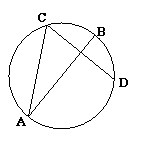
15.(几何证明选讲选做题) 如图,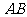 、
、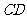 是圆
是圆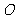 的两条弦,且
的两条弦,且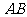
是线段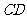 的中垂线,已知线段
的中垂线,已知线段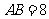 ,
,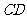 =
=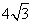 ,则线段
,则线段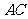 的长
的长
度为 .
(一)必做题(11-13题)
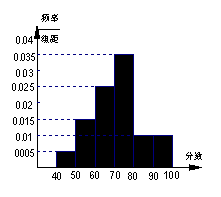
11.统计1000名学生的数学模块(一)水平测试成绩,得到样本频率分布直
方图如右图示,规定不低于60分为及格,不低于80分为优秀,则及格人数
是 ;优秀率为 .
12.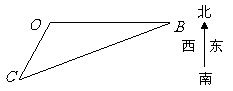 如图,海平面上的甲船位于中心
如图,海平面上的甲船位于中心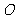 的南偏西
的南偏西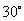 , 与
, 与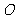 相距
相距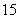 海里的
海里的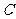 处.
处.
现甲船以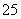 海里
海里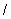 小时的速度沿直线
小时的速度沿直线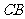 去营救位于中心
去营救位于中心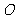 正东方向
正东方向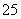 海里的
海里的 处的乙船,甲船需要 小时到达
处的乙船,甲船需要 小时到达 处.
处.
13.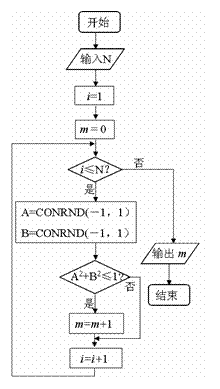 如右的程序框图可用来估计圆周率
如右的程序框图可用来估计圆周率 的值.设
的值.设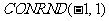 是产生随机数的函数,它能随机产生区间
是产生随机数的函数,它能随机产生区间 内的任何一个数,如果输入1200,输出的
内的任何一个数,如果输入1200,输出的
结果为943,则运用此方法,计算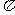 的近似值为
.(保留四位有效数字)
的近似值为
.(保留四位有效数字)
10.已知命题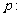 “
“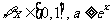 ”,
”,
 命题
命题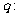 “
“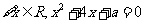 ”,
”,
若命题“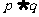 ” 是真命题,则实数
” 是真命题,则实数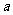 的取值范围是( ).
A.
的取值范围是( ).
A.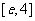 B.
B.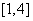 C.
C. D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com