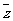4.共轭复数：当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数.虚部不等于的两个共轭复数也叫做共轭虚数，即z＝a+bi与＝a－bi互为共轭复数.

10.常用结论：

① ，；

② ，；

③

④ 设为1的立方虚根，即，则

　 ，　　　　　　　 ，

(2008福建-理1) 若复数是纯虚数，则实数a的值为(　)

A．1　　　　　　　　　　　　　 B．2　　　　　　　　　　　　　　 C．1或2　　　　　　　　　　 D．-1

[解析] 得或,且，得，选B．

[点评] 本题主要考查复数的概念，注意纯虚数一定要使实部为0且虚部不为0．

[练习] ①(全国Ⅰ-理2)设是实数，且是实数，则(　)

A．　　　　　 　　 　　B． 　　　　　 　　　　 C．　 　　　　 　　　D．

②(课本)复数与的积是为实数的充要条件是(　 )

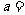A．　 B．　　C．　　D．

③ (课本)如果为纯虚数，那么实数的值为(　)

A．1　　　　　　　　　　　　　 B．2　　　　　　　　　　　　　　 　 C．　　　　　　　　　 　 D．1或

( 2006浙江-理2)已知其中是实数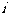，是虚数单位，则 (　 )

A．1+2i　　　　　　　 B． 1-2i　　　　 C．2+i　　　　　　　 D．2-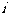

[解析] 由已知，得，则，解得，故选C．

[点评]在两个复数相等的条件中，注意前提条件是、、、，即当、、

特别地： ．

[警示] 　两个复数，如果不全是实数时，不能比较它们的大小．

3.复数相等：

如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等.这就是说，如果，，，，那么 ，．

②积为

即两个复数相乘，类似两个多项式相乘，只需把运算的结果中的换成，并且把实部与虚部分别合并即可.两个复数的积仍然是一个复数.

③商为

(ⅰ)方程思想：

设复数 (、)，除以 (，)，其商为(、)，即　 ，

∴

∵

∴

由复数相等定义可知解这个方程组，得

于是有:

(ⅱ)分母实数化：

.

∴(

④ 运算律：

加法运算满足交换律:

加法运算满足结合律:

乘法满足运算律：　 　

2.复数的分类：

对于复数，当且仅当时，复数是实数；当时，复数叫做虚数；当且时，叫做纯虚数；当且仅当时，就是实数．

① 复数分类系统表：

②复数集与其它数集之间的关系：．

1.复数的定义：

形如的数叫复数，叫复数的实部，叫复数的虚部．全体复数所成的集合叫做复数集，用字母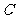表示．注意虚部是一个实数，即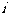的系数，而不是虚数部分．

[详释]虚数单位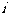的理解：

①　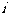的平方等于，即；

②　实数可以与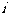进行四则运算，进行四则运算时，原有加、乘运算律仍然成立；

③　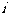与－1的关系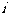：是－1的一个平方根，即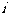是方程的一个根，方程的另一个根是；

④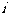的周期性：,,,

3．了解从自然数系到复数系的关系及扩充的基本思想

复数的概念及代数形式的运算.

2．掌握复数代数形式的运算法则，能进行复数代数形式的加法、减法、乘法、除法运算；

1.了解复数的有关概念及复数的代数表示和几何意义；

13. 把下列句子组成前后衔接、意思完整的一段话。(只写句子的序号)(2005年全国高考题III)

①出现在我们面前的是一座美丽的小城。

②城中有一条小河流过，河水清澈见底。

③到了札兰屯，原始森林的气氛就消失了。

④白砖绿瓦的屋舍悠然地倒映在水中。

⑤走出小城，郊外风景幽美，绿色的丘陵上长满了柞树。

⑥丛生的柳树散布在山丘脚下。

答：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 。