
3. 若互不相等的实数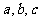 成等差数列,
成等差数列, 成等比数列,且
成等比数列,且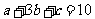 ,则
,则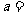 ____ .
____ . 
2. 设等比数列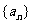 的公比为q,前n项和为
的公比为q,前n项和为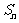 ,若
,若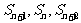 成等差数列,则
成等差数列,则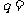 .
. 
1. 设数列{an}的通项为an=2n-7(n∈N*),则|a1|+|a2|+…+|a15|= . 153
10. 解:(Ⅰ)由题意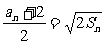 ,an>0令n=1时,
,an>0令n=1时,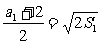 S1=a1 解得a1=2,
S1=a1 解得a1=2,
(Ⅱ)由题意有,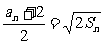 (n∈N*) 整理得Sn=
(n∈N*) 整理得Sn= (an+2)2 由此得Sn+1=
(an+2)2 由此得Sn+1= (an+1+2)2
(an+1+2)2
所以an+1=Sn+1-Sn=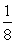 [(an+1+2)2-(an+2)2] 整理得(an+1+an)(an+1-an-4)=0
[(an+1+2)2-(an+2)2] 整理得(an+1+an)(an+1-an-4)=0
由题意知an+1+an≠0,所以an+1-an=4 即数列{an}为等差数列,其中a1=2,公差d=4,
所以an=a1+(n-1)d=2+4(n-1) 即通项公式an=4n-2.
(Ⅲ)令cn=bn-1, 则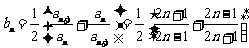
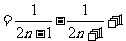
b1+b2+…+bn =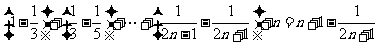
10. 设{an}是正数组成的数列,其前n项和为Sn,并且对所有自然数n,an与2的等差中项等于Sn
与2的等比中项.
(Ⅰ)求数列{an}的通项公式 ;(Ⅱ)令bn=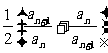 (n∈N*),求
(n∈N*),求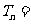 b1+b2+…+bn
.
b1+b2+…+bn
.
9. 已知函数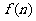 对任意的
对任意的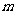 、
、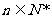 ,都有
,都有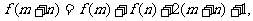
且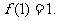
(1)若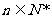 ,试求
,试求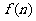 的表达式;
的表达式;
(2)若对于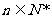 ,且
,且 时,有
时,有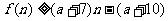 恒成立,求实数
恒成立,求实数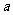 的取值范围.
的取值范围.
解:(I)令m=1,则
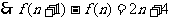
将上面各式相加得: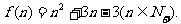
(II)
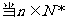 ,且
,且 时,不等式
时,不等式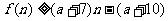 恒成立,
恒成立,
即为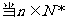 ,且
,且 时不等式
时不等式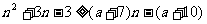 恒成立,
恒成立,
即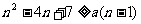 恒成立,
恒成立, 恒成立,………15分
恒成立,………15分
又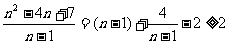 (当且仅当
(当且仅当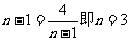 时取“=”)…12分
时取“=”)…12分
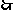
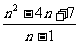 的最小值是2,故
的最小值是2,故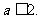
8. 已知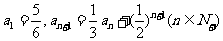 ,数列
,数列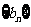 满足:
满足: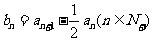 .
.
(1)求证: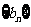 为等比数列; (2) 求数列
为等比数列; (2) 求数列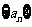 的通项公式 .
的通项公式 .
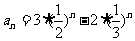 状元之路S1,P165,P246
状元之路S1,P165,P246
7. 解:设等差数列{an}的首项为a,公差为d,则an=a+(n-1)d, 前n项和为Sn=na+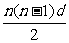 ,
,
由题意得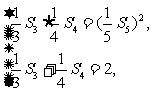 其中S5≠0. 于是得
其中S5≠0. 于是得 解得
解得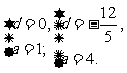
由此得an=1;或an=4- (n-1)=
(n-1)=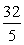 -
- n. 经验证an=1时,S5=5,或an=
n. 经验证an=1时,S5=5,或an=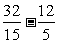 n时,
n时,
S5=-4,均适合题意.
故所求数列通项公式为an=1,或an=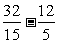 n.
n.
7. 设Sn是等差数列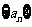 前n项的和,已知
前n项的和,已知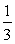 S3与
S3与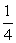 S4的等比中项为
S4的等比中项为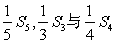 的等差中项
的等差中项
为1,求等差数列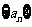 的通项an.
的通项an.
6. 已知 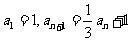 ,则
,则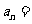 ______________ .
______________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com