
6.(2006年湖南省理科高考题)差数列 满足
满足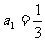 ,且对任意正整数m,n,都有
,且对任意正整数m,n,都有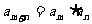 ,则
,则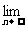 (
( )=( )
)=( )
A. 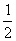 B.
B.
 C.
C.
 D.
D.
5. 已知函数 ,且
,且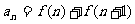 ,则
,则
 ( )
( )
A. 0 B. 100 C. –100 D. 10200
4. 数列1,-1,1,-1,…的通项公式在以下四个式子中可以是( )
①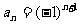 ②
②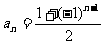
③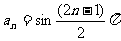 ④
④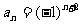
A. ① ② B. ① ③ C. ② ③ D.③ ④
3. 数列 前n项和
前n项和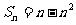 ,则当
,则当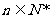 且n≥2时一定有( )
且n≥2时一定有( )
A. 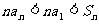 B.
B.
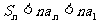
C. 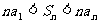 D.
D.
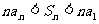
2. 已知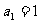 ,
,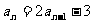 ,则
,则 等于( )
等于( )
A. 21 B. –29 C. 31 D. -17
1. 已知2006是数列6,11,16,21,…中的一项,那么它是( )
A. 第399项 B. 第400项 C. 第401项 D. 第402项
(四)作业:
1.在正方体ABCD-A1B1C1D1中,求二面角A1-BD-A的正切值.
2.已知E是正方体ABCD-A1B1C1D1的棱BC的中点,求平面B1D1E与平面BB1C1C所成的二面角的正切值.
3.已知PA、PB、PC是空间三条直线,若∠APB=∠BPC=∠CPA=60°,求二面角B-PA-C的平面角的余弦值.
4.在120°的二面角α- -β的面α、β内分别有A、B两点,且A、B到棱的距离AC、BD分别是2和4,AB=10,求:(1)直线AB与棱
-β的面α、β内分别有A、B两点,且A、B到棱的距离AC、BD分别是2和4,AB=10,求:(1)直线AB与棱 所成角的正弦值.
所成角的正弦值.
(2)直线AB与面β所成角的正弦值.
(三)巩固练习
1.已知二面角α- -β为30°,P是平面α内一点,P到β的距离为1,则P在β内的射影到
-β为30°,P是平面α内一点,P到β的距离为1,则P在β内的射影到 的距离是_______
的距离是_______
2.P是二面角α- -β两个半平面外一点,PA⊥α于A,PB⊥β于B,且∠APB=30°,则此二面角的度数是_________
-β两个半平面外一点,PA⊥α于A,PB⊥β于B,且∠APB=30°,则此二面角的度数是_________
3.已知△ABD和△ABC是有公共底边AB的两个等腰三角形,∠ADB=90°,二面角D-AB-C为60°,AB=16,BC=10,求CD的长.
4.已知二面角A-BC-A1的平面角为锐角α,AA1⊥平面A1BC,△ABC和△A1BC的面积分别为S和S1,求证:S1=S cosα
cosα
(二)应用举例:
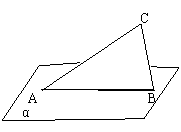 例1. 如图,Rt△ABC斜边AB在平面α内,点C在α外,AC、BC与α所成的角分别为30°和45°。求平面ABC与平面α所成的角的大小.
例1. 如图,Rt△ABC斜边AB在平面α内,点C在α外,AC、BC与α所成的角分别为30°和45°。求平面ABC与平面α所成的角的大小.
解:
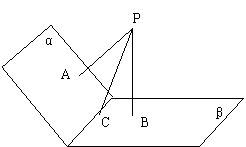 例2. 已知一个点到二面角的两个半平面的距离分别为√2a和√3a,且到棱的距离为2a,求这个二面角的大小.
例2. 已知一个点到二面角的两个半平面的距离分别为√2a和√3a,且到棱的距离为2a,求这个二面角的大小.
解:当P在二面角为α-l-β的内部时,
解:
当P在二面角为α-l-β的外部时,

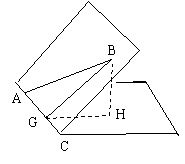 例3. 如图,山坡的倾斜度是60°,山坡上有一条直道AB,它和坡脚的水平线AC的夹角是30°,沿着这条山路上山,行走100米后升高多少米?
例3. 如图,山坡的倾斜度是60°,山坡上有一条直道AB,它和坡脚的水平线AC的夹角是30°,沿着这条山路上山,行走100米后升高多少米?
解:作BH⊥水平平面,H为垂足,在平面ACH内作HG⊥AC于G,连结BG,则BG⊥AC,∴∠BGH就是坡面ABC与水平面ACH所成的二面角的平面角.
(一)二面角的概念:
1.半平面--平面内的一条直线把平面分成两部分,其中的每一部分都叫做半平面(类似于“射线)。
2.二面角--从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线直线叫做二面角的棱,半平面叫做二面角的面。
与平面角进行类比:
⑴结构:半平面-直线-半平面;
⑵表示法:二面角α-l-β;
⑶范围:(0°,180°];
⑷画法:①平卧式,②竖立式。
3.二面角的平面角------以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
强调:(1)二面角的大小可以用它的平面角来度量,即二面角的平面角是多少度,就说这个二面角是多少度。
(2)平面角是直角的二面角叫做直二面角。
(3)二面角的平面角的作法通常有以下两种:
法一:定义 法二:三垂线法


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com