
18. 解:由已知,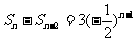 (n≥3)
(n≥3)
∴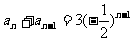
将此式两边同乘以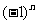 ,得
,得
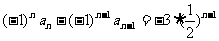
设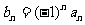 ,则上式变为
,则上式变为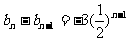 (
(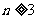 )
)
∴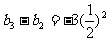
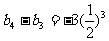
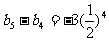
…
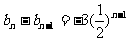
将上面各式相加,得

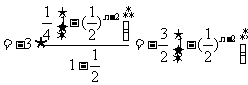
∴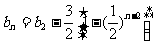
∵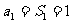 ,
, 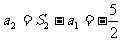
∴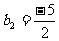
∴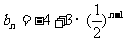 (n≥3)
(n≥3)
又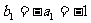 ,
, 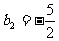 满足上式。
满足上式。
∴
∴
17. 解:n=1时 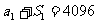 ,∵
,∵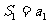 , ∴
, ∴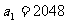 。
。
n≥2时,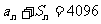
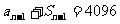
两式相减,得
即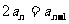
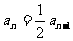
∴ 是以2048为首项,以
是以2048为首项,以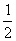 为公比的等比数列
为公比的等比数列
∴ 的通项公式为
的通项公式为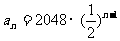
(2)∵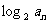 =
=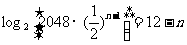
∴数列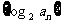 是首项为11,公差为-1的等差数列。
是首项为11,公差为-1的等差数列。
∴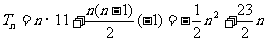
令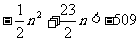

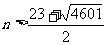 ∵
∵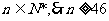
∴从第46项起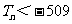 。
。
16. 解: 时,
时,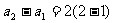
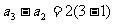
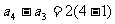
…
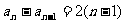
将上面各式相加,得
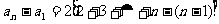

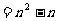
∵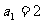 ,∴
,∴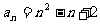
∵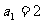 也适合上式,
也适合上式,
∴数列的通项公式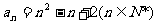
说明:本题还可以先由给出的递推公式求出前几项,猜想出通项公式,再用数学归纳法证明。
15. 解:(1)令 解得n=2, ∴
解得n=2, ∴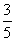 是数列中第2项。
是数列中第2项。
令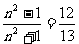 解得n=5, ∴
解得n=5, ∴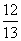 是数列中第5项。
是数列中第5项。
(2)令n=11,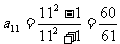
令n=25, 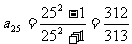 。
。
∴ 分别为
分别为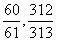 。
。
14. 2600 提示:由数列的递推公式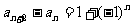 可知,数列的各奇数项全相等,且等于1,因此
可知,数列的各奇数项全相等,且等于1,因此 ,又数列的偶数项组成一个以2为公差的等差数列,∵
,又数列的偶数项组成一个以2为公差的等差数列,∵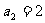 ,∴
,∴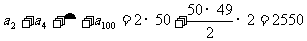 ∴
∴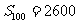 。
。
13. 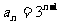 提示:n≥2时,用
提示:n≥2时,用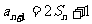 与
与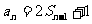 两式相减,可得
两式相减,可得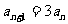 ,又知
,又知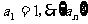 是以1为首项,3为公比的等比数列。
是以1为首项,3为公比的等比数列。
12. 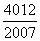 提示:
提示:
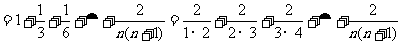
 ,将n=2006代入即可。
,将n=2006代入即可。
11.  提示:依递推关系式,分别代入n=3,n=4即可。
提示:依递推关系式,分别代入n=3,n=4即可。
10. 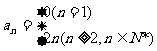 提示:令n=1,得
提示:令n=1,得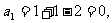 令n≥2
令n≥2
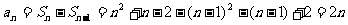 。
。
9. 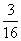
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com