
8.市政公司为绿化一段沿江风光带,计划购买甲、乙两种树苗共500株,甲种树苗每株50元,乙种树苗每株80元.有关统计表明:甲、乙两种树苗的成活率分别为90%和95%.
(1)若购买树苗共用了28 000元,求甲、乙两种树苗各多少株?
(2)若购买树苗的钱不超过34 000元,应如何选购树苗?
(3)若希望这批树苗的成活率不低于92%,且购买树苗的费用最低,应如何选购树苗.
7.某商场用36万元购进 两种商品,销售完后共获利6万元,其进价和售价如下表:
两种商品,销售完后共获利6万元,其进价和售价如下表:
|
|
 |
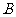 |
|
进价(元/件) |
1200 |
1000 |
|
售价(元/件) |
1380 |
1200 |
(注:获利=售价-进价)
(1)该商场购进 两种商品各多少件;
两种商品各多少件;
(2)商场第二次以原进价购进 两种商品.购进
两种商品.购进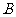 种商品的件数不变,而购进A种商品的件数是第一次的2倍,
种商品的件数不变,而购进A种商品的件数是第一次的2倍, 种商品按原售价出售,而
种商品按原售价出售,而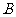 种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81 600元,
种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81 600元,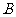 种商品最低售价为每件多少元?
种商品最低售价为每件多少元?
6.为净化空气,美化环境,市冷水滩区在许多街道和居民小区都种上了玉兰和樟树,冷水滩区新建的某住宅区内,计划投资1.8万元种玉兰树和樟树共80棵,已知某苗圃负责种活以上两种树苗的价格分别为:玉兰树300元/棵,樟树200元/棵,问可种玉兰树和樟树各多少棵?
5. 已知 是一元二次方程
是一元二次方程 的一个解,且
的一个解,且 ,求
,求 的值.
的值.
4.中国人民银行宣布,从2007年6月5日起,上调人民币存款利率,一年定期存款利率上调到3.06%.某人于2007年6月5日存入定期为1年的人民币5000元(到期后银行将扣除20%的利息锐).设到期后银行应向储户支付现金x元,则所列方程正确的是( )
(A)
(B)
(C)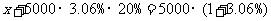
(D)
3.不等式组 的解集是( )
的解集是( )
(A) (B)
(B)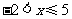
(C) (D)无解
(D)无解
2.分式方程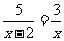 的解为
的解为 ____________.
____________.
1.方程组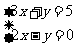 的解是____________.
的解是____________.
21.解:⑴设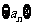 的公差为
的公差为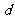 ,则
,则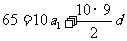 ,又
,又 ,得
,得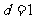 ,从而
,从而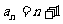
故 .
……4分
.
……4分
⑵ ,
, ,
,
 . ……8分
. ……8分
⑶由(2)猜想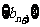 递减,即猜想当
递减,即猜想当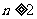 时,
时, . ……10分
. ……10分
考察函数 ,则
,则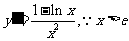 时,
时, ,
,
故 在
在 上是减函数,而
上是减函数,而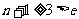 ,
……12分
,
……12分
所以 ,即
,即 .
.
猜想正确,因此,数列 的最大项是
的最大项是 . ……14分
. ……14分
[链接高考]自从导数走进高考试题中,就和函数形影不离,并且与方程、数列、解析几何以及立体几何等分支的知识联姻,成为高考的一道亮丽的风景线.预计导数还会与平面向量、概率与统计等分支的知识联合,展示其独特的魅力.
20. 解:⑴由题意可知,区域是以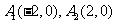 及点
及点 为顶点的三角形,
为顶点的三角形,
∵ ,∴
,∴ 为直角三角形.
……2分
为直角三角形.
……2分
∴外接圆C以原点O为圆心,线段A1A2为直径,故其方程为 .
.
∵2a=4,∴a=2.
又 ,∴
,∴ ,可得
,可得 .
.
∴所求椭圆C1的方程是 . ……6分
. ……6分
⑵点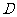 坐标为
坐标为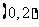 ,故点
,故点 坐标为
坐标为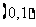 ,显然
,显然 可满足要求;
可满足要求;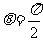 时不满足题意.
……8分
时不满足题意.
……8分
当 时,设
时,设 的方程为
的方程为 ,
,
由 ,得
,得 ,
,
由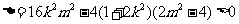 ,得
,得 ;
……10分
;
……10分
设 ,
, 的中点为
的中点为 ,
,
则 .
.
 ,即
,即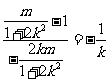 ,解得
,解得 .
.
……12分
 ,得
,得 .
.
综上,直线 与
与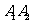 夹角
夹角 的正切值的取值范围是
的正切值的取值范围是 .
……14分
.
……14分
[链接高考] 圆锥曲线的综合大题, 主要考查解析几何的有关知识,以及分析问题与解决问题的能力. 值得引起重视的一个现象是,经常出现一条或几条直线与两种圆锥曲线(包括圆)的位置关系问题,同时要注意其与平面几何、平面向量以及导数的知识的综合命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com