
3、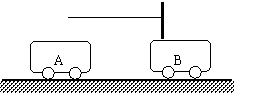 如图所示,水平面上停放着A、B两辆小车,质量分别为M和m,M>m,两车相距为L。人的质量也是m,另有不计质量的一根竹竿和一根细绳。第一次人站在A车上,竿插在B车上;第二次人站在B车上,竿插在A车上。两种情况下,人用同样大小的力拉绳子,使两车相遇。设阻力可忽略不计,两次小车从开始运动到相遇的时间分别为t1和t2,则( )
如图所示,水平面上停放着A、B两辆小车,质量分别为M和m,M>m,两车相距为L。人的质量也是m,另有不计质量的一根竹竿和一根细绳。第一次人站在A车上,竿插在B车上;第二次人站在B车上,竿插在A车上。两种情况下,人用同样大小的力拉绳子,使两车相遇。设阻力可忽略不计,两次小车从开始运动到相遇的时间分别为t1和t2,则( )
A.t1>t2 B.t1<t2
C.t1=t2 D.条件不足,无法判断
2、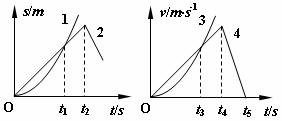 如图所示的速度-时间和位移-时间图像中给出了四条图线,关于它们的物理意义,下列描述正确的是( )
如图所示的速度-时间和位移-时间图像中给出了四条图线,关于它们的物理意义,下列描述正确的是( )
A.图线1表示物体做曲线运动
B.s-t图线中t1时刻v1>v2
C.v-t图线中0至t3时间内3和4平均速度相等
D.两图像中t2和t4时刻分别表示2和4开始反向运动
1、下列说法中不正确的是( )
A.根据速度定义式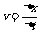 ,当
,当 非常非常小时,
非常非常小时,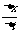 就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法。
就可以表示物体在t时刻的瞬时速度,该定义应用了极限思想方法。
B.在探究加速度、力和质量三者之间关系时,先保持质量不变研究加速度与力的关系,再保持力不变研究加速度与质量的关系,该实验应用了控制变量法。
C.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法。
D.在不需要考虑物体本身的大小和形状时,用质点来代替物体的方法叫假设法
22.(本小题满分13分)
已知 设
设
P:函数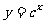 在R上单调递减.
在R上单调递减.
Q:不等式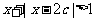 的解集为R,如果P和Q有且仅有一个正确,求
的解集为R,如果P和Q有且仅有一个正确,求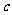 的取值范围.
的取值范围.
21.(本题满分13分)
某地区上年度电价为0.80元/kW· h,年用电量为a kW· h.本年度计划将电价降到0.55元/kW·h至0.75元/kW·h之间,而用户期望电价为0.4元/kW·h.经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k).该地区电力的成本为0.3元/kW·h.
(1) 写出本年度电价下调后,电力部门的收益y与实际电价x的函数关系式.
(2) 设k=0.2a,当电价最低定为多少时,仍可保证电力部门的收益比上年至少增长20%? (注:收益=实际用电量×(实际电价-成本价)).
20.(本题满分12分)
设函数f(x) =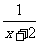 +lg
+lg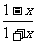 .
.
(1)试判断函数f(x)的单调性 ,并给出证明;
(2)若f(x)的反函数为f-1 (x) ,证明方程f-1 (x)= 0有唯一解.
19.(本题满分12分)
“依法纳税是每个公民应尽的义务”,国家征收个人工资、薪金所得税是分段计算的:总收入不超过800元的,免征个人工资、薪金所得税;超过800元部分需征税,设纳税所得额(所得额指月工资、薪金中应纳税的部分)为x,x=全月总收入-800(元),税率见下表:
|
级数 |
全月应纳税所得额x |
税率 |
|
1 |
不超过500元部分 |
5% |
|
2 |
超过500元至2000元部分 |
10% |
|
3 |
超过2000元至5000元部分 |
15% |
|
… |
… |
… |
|
9 |
超过100000元部分 |
45% |
(1)若应纳税额为f(x),试用分段函数表示1~3级纳税额f(x)的计算公式;
(2)某人2004年10月份工资总收入为4000元,试计算这个人10月份应纳个人所得税多少元?
18.(本题满分12分)
已知f(x)=x2+(2+lga)x+lgb,f(-1)=-2且f(x)≥2x恒成立,求a、b的值.


17.(本题满分12分)
设A={x∈R|2≤ x ≤ π},定义在集合A上的函数y=logax (a>0,a≠1)的最大值比最小值大1,求a的值.

16.已知函数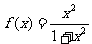 ,那么
,那么
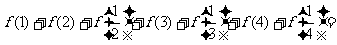 ____________.
____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com