(四)“强行终止试验”和“自然终止试验”，需注意①分析“实验次数”②反面计算强行终止概率。

例：A,B两位各有5张卡片，现以投掷硬币形式进行游戏，当正面朝上时，A赢得B一张卡片，否则B赢得A一张卡片，规定掷币次数达9次时，或在此前某人已赢得所有卡片时终止游戏，设表示游戏终止时掷币次数，求的概率。(理：求的分布列)

(三)分解成独立积，必须深入考查每个子事件有无特别要求，甚至是“是否不管发生与否”。

例：甲、乙两人投篮，一次投篮中，甲中的概率为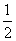，乙中的概率为，规则如下：甲先投，每人投中就继续投，否则就给另一个投。若两人总共投4次，乙投了2次的概率。

(二)复杂事件分解成简单事件的基本方法：一是分解为“互斥和”(即分类)，二是分解为“独立积”(即分步)

例：某同学参加知识竞赛，需回答3个问题，规定：答对第一、二、三个问题分别得100分，100分，200分，答错得零分，假设这名同学答对第一、二、三个问题的概率分别为0.8,0.7,0.6，且各题间无影响，求这个同学得300分得概率。

(一)再认基础：①“A+B”发生“A,B”至少一个发生。

②“A,B”互斥在一次试验中，“A,B”不能同时发生。

(但可以都不发生)

③“A，B”互斥时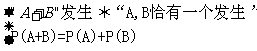

④“A·B”发生“A,B同时发生”

⑤A、B独立A发不发生，都对P(B)无影响。

⑥A、B独立时，P(AB)=P(A)P(B)

3．“当较复杂时，应该有耐心”，一般有三种途径算

途径1：求要分若干步，分步完成

例：用黄、蓝、白三色粉刷6间办公室，每间办公室只能用一种颜色粉刷，问一种颜色刷3间，一种颜色刷2间，一种颜色刷1间的概率？

途径2：求要分若干类，分类完成

例：5位同学乘同一辆大车，该火车有六节车厢；

1)5位同学恰好坐在指定的三节车厢的概率？

2)恰有2位同学坐同一车厢的概率？

途径3：排除法

例：口袋中装有10个相同的球，5个球标有数字0，5个球标有数字1，若从中摸出5个，那么摸出5个球所标的数字和小于2或大于3的概率？

2．“当某些位置有特别要求，应该用排列”

例：一个盒中装有3只螺口灯泡与 7口卡口灯泡，电工师傅每次从中任取一只并不放回，

　 1)则他直到第3次才取得卡口灯泡的概率是多少？

　 2)最后一只螺口灯泡在第六次被取出的概率为多少？

1．“要么都有序，要么都无序”

例：一口袋内7个白球，3个黑球，现从中摸出两个球，问一白一黑的概率？

16．(15分)一质量为m的质点，系于长为R的轻绳的一端，绳的另一端固定在空间的O点，假定绳是不可伸长的、柔软且无弹性的。今把质点从O点的正上方离O点的距离为的O₁点以水平的速度抛出，如图所示。试求；

(1)轻绳即将伸直时，绳与竖直方向的夹角为多少？

(2)当质点到达O点的正下方时，绳对质点的拉力为多大？

15．(13分)如图所示，光滑水平面上静止放着长L=1m，质量为M=3kg的木块(厚度不计)，一个质量为m=1kg的小物体放在木板的最右端，m和M之间的动摩擦因数μ=0.1，今对木板施加一水平向右的拉力F，(g取10m/s²)

(1)为使小物体不掉下去，F不能超过多少？

(2)如果拉力F=10N恒定不变，求小物体所能获得的最大速率？

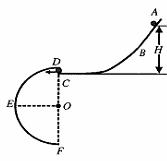
14．(13分)如图所示，ABC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0.4m的半圆形轨道，其直径DF沿竖直方向，C、D可看作重合。现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放，

(1)若要使小球经C处水平进入轨道DEF且能沿轨道运动，H至少要有多高？

(2)若小球静止释放处离C点的高度h小于(1)中H的最小值，小球可击中与圆心等高的E点，求h。(取g=10m/s²)