
4. 设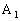 ,
,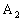 是椭圆
是椭圆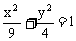 的长轴两个端点,
的长轴两个端点,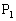 ,
,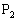 是垂直于
是垂直于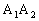 的弦的端点,则直线
的弦的端点,则直线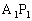 与
与 交点的轨迹方程是
交点的轨迹方程是
A. 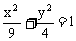 B.
B. 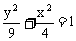 C.
C. 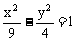 D.
D. 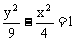
3. 已知A(0,7),B(0,-7),C(12,2),以C为一个焦点作过A、B的椭圆,椭圆的另一个焦点F的轨迹方程是
A. 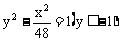 B.
B.
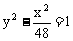 C.
C.
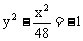 D.
D. 
2. 已知点P(-1,2),点M在直线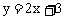 上运动,Q是线段MP延长线上一点,且|MP|=|PQ|,则Q点的轨迹方程是
上运动,Q是线段MP延长线上一点,且|MP|=|PQ|,则Q点的轨迹方程是
A. 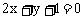 B.
B. 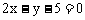 C.
C. 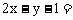 0 D.
0 D. 
1. 若△ABC的两个顶点B、C的坐标分别是(-1,0)和(2,0),而顶点A在直线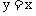 上移动,则△ABC的重心G的轨迹方程是
上移动,则△ABC的重心G的轨迹方程是
A. 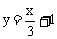 B.
B. 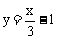 C.
C. 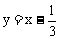 D.
D. 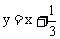
4、描绘曲线的图形要注意曲线范围的研究及曲线的对称性,或利用基本的曲线图形.
[典型例题]
例1. (直接法求曲线方程)
△ABC的顶点A固定,点A的对边BC的长是 ,边BC上的高为b,边BC沿一条定直线移动,求△ABC外心的轨迹方程。
,边BC上的高为b,边BC沿一条定直线移动,求△ABC外心的轨迹方程。
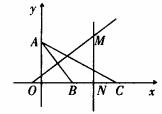
解析:以BC所在定直线为x轴,过A作x轴的垂线为y轴,建立直角坐标系,则A点的坐标为(0,b),设△ABC的外心为M(x,y)。
作MN⊥BC于N,则MN是BC的垂直平分线。
∵|BC|=2a,∴|BN|=a,|MN|=|y|,
又M是△ABC的外心,
∴M
而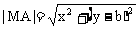 ,
,
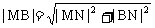
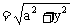 ,
,
∴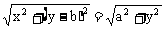 。
。
化简,得所求轨迹方程为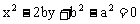 。
。
点评:(1)本例是一道典型的用直接法求曲线方程的题目,难度中等,解本题的关键是建立适当的直角坐标系,充分利用三角形外心的性质。
(2)本例的易错处是利用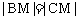 列方程,而化简后会发现得到的是一个恒等式,原因是在求
列方程,而化简后会发现得到的是一个恒等式,原因是在求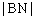 的长度时已利用了|BM|=|CM|这个等量关系。
的长度时已利用了|BM|=|CM|这个等量关系。
(3)对于本例,在建立直角坐标系时,也可把BC边所在定直线作为y轴,过A点与定直线垂直的直线作为x轴,此时方程将有所变化。
例2. (代入法求曲线方程)
已知△ABC的顶点A,B的坐标分别为A(0,0),B(6,0),顶点C在曲线 上运动,求△ABC重心的轨迹方程。
上运动,求△ABC重心的轨迹方程。
解析:设G(x,y)为所求轨迹上任一点,顶点C的坐标为 ,
,
则由重心坐标公式,得: 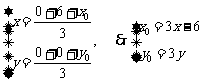
因为顶点C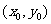 在曲线
在曲线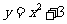 上,所以有
上,所以有
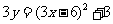
整理,得: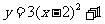 ,即为所求轨迹方程。
,即为所求轨迹方程。
点评:(1)本例是求轨迹方程中的常见题型,难度适中,本题解法称为代入法(或相关点法),此法适用于已知一动点的轨迹方程,求另一动点轨迹方程的问题。
(2)应注意的是,本例中曲线 上没有与A,B共线的点,因此,整理就得到轨迹方程;若曲线方程为
上没有与A,B共线的点,因此,整理就得到轨迹方程;若曲线方程为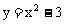 ,则应去掉与A,B共线时所对应的重心坐标。
,则应去掉与A,B共线时所对应的重心坐标。
例3. (参数法求曲线方程)
抛物线 的焦点为F,过点(0,-1)作直线交抛物线于不同两点A,B,以AF,BF为邻边作平行四边形FARB,求顶点R的轨迹方程。
的焦点为F,过点(0,-1)作直线交抛物线于不同两点A,B,以AF,BF为邻边作平行四边形FARB,求顶点R的轨迹方程。
解析:设直线:AB:y=kx-1,A(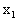 ,
, ),B(
),B(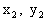 ),R(x,y),由题意F(0,1)。
),R(x,y),由题意F(0,1)。
由 ,可得
,可得 。
。
∴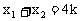 。
。
又AB和RF是平行四边形的对角线,
∴ ,
,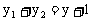 。
。
而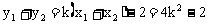 ,
,
∴ ,消去k得
,消去k得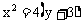 。
。
由于直线和抛物线交于不同两点,
∴△=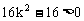 ,
,
∴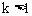 或
或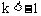 。
。
∴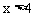 或
或 。
。
∴顶点R的轨迹方程为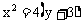 ,且
,且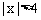 。
。
点评:如果求轨迹的动点P(x,y)的坐标之间的关系不易找到,也没有相关信息可用时,可先考虑将x,y用一个或几个参数来表示,消去参数得轨迹方程,此法称为参数法。参数法中常选变角、变斜率等为参数。注意参数的取值范围对方程中的x和y范围的影响。
例4. (2006广东,18,14分)设函数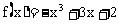 分别在
分别在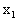 、
、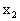 处取得极小值、极大值,
处取得极小值、极大值,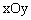 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为 、
、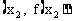 。该平面上动点P满足
。该平面上动点P满足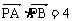 ,点Q是点P关于直线
,点Q是点P关于直线 的对称点。求:
的对称点。求:
(1)点A、B的坐标;
(2)动点Q的轨迹方程。
解析:(1)对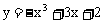 求导得
求导得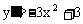 ,
,
令y′=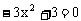 解得
解得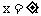 。
。
当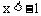 时,
时, ;
;
当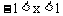 时,
时, ;
;
当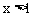 时,
时, ;
;
所以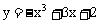 在
在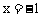 处取得极小值0,在
处取得极小值0,在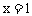 处取得极大值4,即点A、B的坐标分别为(-1,0)、(1,4)。
处取得极大值4,即点A、B的坐标分别为(-1,0)、(1,4)。
(2)解法一:设P(x,y),则
 ,
,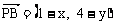 ,
,
故由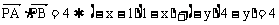
即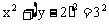 。
。
所以P的轨迹是以C(0,2)为圆心,半径为3的圆。
∵点Q是点P关于直线 的对称点。
的对称点。
∴动点Q的轨迹是一个以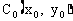 为圆心,半径为3的圆,其中
为圆心,半径为3的圆,其中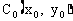 是点C(0,2)关于直线
是点C(0,2)关于直线 的对称点,即直线
的对称点,即直线 过
过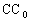 的中点,且与
的中点,且与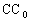 垂直,于是有
垂直,于是有
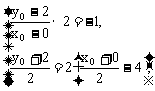
即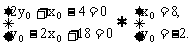
故动点Q的轨迹方程为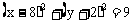 。
。
解法二:设P(x,y),则
 ,
,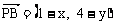 ,
,
故由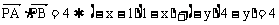 ,
,
即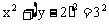 。(*)
。(*)
设点Q的坐标为Q(u,v),
∵Q、P关于直线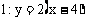 对称,
对称,
∴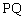 与直线l垂直,于是有
与直线l垂直,于是有
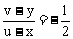 。(1)
。(1)
因为PQ的中点在l上,所以有
 。(2)
。(2)
由(1)、(2)可解得

代入方程(*)得
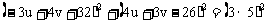 ,
,
化简得: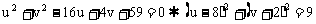 。
。
故动点Q的轨迹方程为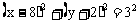 。
。
[模拟试题](答题时间:40分钟)
3、求曲线的方程与求轨迹是有不同要求的,若是求轨迹则不仅要求出方程,而且还需要说明和讨论所求轨迹是什么样的图形,在何处,即图形的形状、位置、大小都需说明、讨论清楚。求“轨迹”时首先要求出“轨迹方程”,然后再说明方程的轨迹图形,最后“补漏”和“去掉增多”的点,若轨迹有不同的情况,应分别讨论,以保证它的完整性.
2、求曲线轨迹方程的常用方法:
(1)直接法:如果题目中的条件有明显的等量关系或者可以推出某个等量关系,即可用求曲线方程的五个步骤直接求解.
(2)定义法:如果动点的轨迹满足某种已知曲线的定义,则可依定义写出轨迹方程.
(3)代入法:如果动点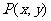 依赖于另一动点
依赖于另一动点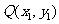 ,而
,而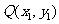 又在某已知曲线上,则可先列出关于
又在某已知曲线上,则可先列出关于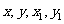 的方程组,利用
的方程组,利用 表示
表示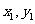 ,把
,把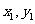 代入已知曲线方程即得所求.
代入已知曲线方程即得所求.
(4)参数法:如果动点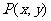 的坐标之间的关系不易找到,可考虑将
的坐标之间的关系不易找到,可考虑将 用一个或几个参数来表示,消去参数即得其轨迹方程.
用一个或几个参数来表示,消去参数即得其轨迹方程.
(5)交轨法:写出动点所满足的两个轨迹方程后,组成方程组消参即可得解,此法常适用于求两动直线交点的轨迹方程.
1、用直接法求曲线方程是解析几何中最重要的方法.在求解时,如果题设条件中未给出坐标,要建立适当的坐标系,选择适当坐标系的原则是“避繁就简”,一般地:
(1)若条件中只出现一个定点,常以该点为坐标原点;
(2)若已知两定点,常以这两定点的中点为原点,以两定点所在的直线为坐标轴;
(3)若已知两条互相垂直的直线,常以它们为坐标轴建立直角坐标系;
(4)若已知一定点和一定直线,常以定点到定直线的垂线段的中点为原点,以点到直线的垂线的反向延长线为x轴建立直角坐标系;
(5)若已知定角.常以定角的顶点为原点,定角的平分线为x轴建立直角坐标;
(6)坐标系建立的不同,同一曲线在不同坐标系中的方程也不同,但它们始终表示同一曲线.
5、求曲线的交点
由曲线方程的定义可知,两条曲线交点的坐标应该是两个曲线方程的公共解,即两个曲线方程组成的方程组的实数解;反过来,方程组有几个解,两条曲线就有几个交点,方程组无解,两条曲线就没有交点.也就是说两条曲线有交点的充要条件是它们的方程所组成的方程组有实数解.可见,求曲线的交点问题,就是求由它们的方程所组成的方程组的实数解问题.
[要点解析]
4、求曲线方程的一般方法(五步法)
求曲线(图形)的方程,一般有下面几个步骤:
(1)建立适当的坐标系,用有序实数对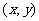 表示曲线上任意一点M的坐标;
表示曲线上任意一点M的坐标;
(2)写出适合条件p的点M的集合P={M| }:
}:
(3)用坐标表示条件 ,列出方程
,列出方程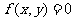 ;
;
(4)化方程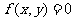 为最简形式;
为最简形式;
(5)说明以化简后的方程的解为坐标的点都在曲线上。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com