
6.以A(x1,y2)、B(x2,y2)为直径的圆的方程是(x-x1)(x-x2)+(y-y1)(y-y2)=0;
5.过圆x2+y2=r2上的点M(x0,y0)的切线方程为:x0x+y0y=r2;
4.Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件 :A=C≠0且B=0且D2+E2-4AF>0;
3.两条平行线Ax+By+C1=0与 Ax+By+C2=0的距离是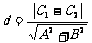 ;
;
2.直线l1:A1x+B1y+C1=0与l2: A2x+B2y+C2=0垂直的充要条件是A1A2+B1B2=0;
1.设三角形的三顶点是A(x1,y1)、B(x2,y2)、C(x3,y3),则⊿ABC的重心G为(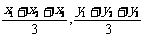 );
);
3.掌握用均值不等式求最值的方法,在使用a+b≥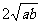 (a>0,b>0)时要符合“一正二定三相等”;注意均值不等式的一些变形,如
(a>0,b>0)时要符合“一正二定三相等”;注意均值不等式的一些变形,如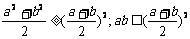 ;
;
2.掌握几类不等式(一元一次、二次、绝对值不等式、简单的指数、对数不等式)的解法,尤其注意用分类讨论的思想解含参数的不等式;勿忘数轴标根法,零点分区间法;
1.掌握不等式性质,注意使用条件;
5.平面向量数量积的坐标表示:
(1)若a=(x1,y1),b=(x2,y2),则a b=x1x2+y1y2;
b=x1x2+y1y2;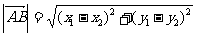 ;
;
(2)若a=(x,y),则a2=a a=x2+y2,
a=x2+y2,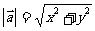 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com