(二)平面角

师：为了对相交平面的相互位置作进一步的探讨，有必要研究二面角的大小问题．如门和墙所在的平面是相交的，但门可以在关上、开一点小缝、开一半、全开等各种位置上，也就是说两平面虽处于相交的位置关系，但相互之间的位置关系还是应当讨论的．为了表示二面角的大小，我们必须引入平面角的定义．

定义：以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角．

师：二面角的大小可以用它的平面角来度量，即二面角的平面角是几度，就说这个二面角是几度．现在我们来思考：

问题1：这样用平面角的度数来表示二面角的度数是否合理？为什么？

生：是合理的．

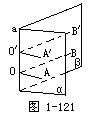
如图1-121，在二面角α-a-β的棱a上任取一点O，在半平面α和β内，从点O分别作垂直于棱a的射线OA、OB，射线OA和OB组成∠AOB，在棱上另取任意一点O＇，按同样的方法作∠A＇O＇B＇，因为OA和OA＇、OB和OB＇都垂直于棱a，所以∠AOB和∠A＇O＇B＇的两边分别平行且方向相同，根据等角定理，得：∠AOB＝∠A＇O＇B＇，即∠AOB的大小是一定的．由于这个唯一性，从而说明这样定义二面角的平面角是合理的，且与点O在棱上的位置无关．

问题2：二面角的平面角必须满足哪几个条件？

生：两个条件．一是平面角的顶点必在棱上；二是平面角的两边分别在二面角的两个面内．

师：平面角是直角的二面角叫直二面角．

在实际生活中，木工用活动角尺测量工件的两个面所成的角时，就是测量这两个角所成二面角的平面角(图见P．40中图1-45)．我国发射的第一颗人造地球卫星的倾角是68.5°，就是说卫生轨道平面与地球赤道平面所成的二面角的平面角是68.5°(图见P．39中图1-43)．

下面请同学们完成例题和练习．

1课时．

3．教学疑点：二面角的平面角必须满足下列两个条件：一是平面角的顶点必在棱上；二是平面角的两边分别在二面角的两个面内．

2．教学难点：如何选取恰当的位置作出二面角的平面角来解题．

1．教学重点：二面角、二面角的平面角的概念．

(三)德育渗透点

让学生认识到研究二面角的问题是人类生产实践的需要，进一步培养学生实践第一的观点．

(二)能力训练点

1．利用类比的方法理解和掌握二面角的有关概念；掌握二面角的平面角的定义．

2．用转化的思维方法将二面角问题转化为其平面角问题，进一步培养学生的空间想象能力和分析、解决问题的能力．

3．通过练习，归纳总结作二面角的平面角的三种方法．

(一)知识教学点

1．二面角的有关概念．

2．二面角的平面角的定义及作法．

55．函数y = f ( x ) = x³+ax²+bx+a²，在x = 1时，有极值10，则a = 　　　　　,b = 　　　。