2．名称：项，序号，一般公式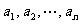，表示法

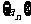
1．数列的定义：按一定次序排列的一列数(数列的有序性)

5．无穷多个数排成一列数：1,1,1,1,…

4．-1的正整数次幂：-1,1,-1,1,…

3．

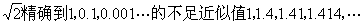
2．正整数的倒数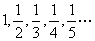　　

1．堆放的钢管　 　4,5,6,7,8,9,10

P．45-46中习题六1、2、3、4、5．

(四)总结

本节课我们学习了二面角，二面角的平面角等有关概念，并学会了如何作二面角的平面角．学习的关键是将二面角的问题转化为其平面角的问题．

(三)练习

例　 如图1-122，山坡的倾斜度(坡面与水平面所成二面角的度数)是60°，山坡上有一条直道CD，它和坡脚的水平线AB的夹角是30°，沿这条路上山，行走100米后升高多少米？

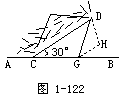
解：已知CD=100米，设DH垂直于过BC的水平平面，垂足为H，线段DH的长度就是所求的高度．在平面DBC内，过点D作DG⊥BC，垂足是G，连结GH．

∵DH⊥平面BCH，DG⊥BC，

∴GH⊥BC．

因此，∠DGH就是坡面DGC和水平平面BCH所成的二面角的平面角，∠DGH＝60°，由此得：

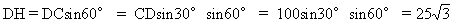
≈43.3(米)．

答：沿直道前进100米，升高约43.3米．

注：在解题中要特别注意书写规范．如：

∵DG⊥BC，GH⊥BC，

∴∠DGH是坡面DGC和水平面BCH所成二面角的平面角．

练习：(P．41-42练习1、2、3、4．)

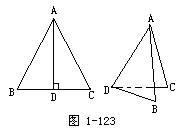
1．拿一张正三角形的纸片ABC，以它的高AD为折痕，折成一个二面角，指出这个二面角的面、棱、平面角．

2．一个平面垂直于二面角的棱，它和二面角的两个面的交线所成的角就是二面角的平面角．为什么？

3．教室相邻两面墙、天花板两两所成的二面角各有多少度？

4．在30°二面角的一个面内有一个点，它到另一个面的距离是10cm，求它到棱的距离．

解：1．如图1-123，二面角B-AD-C中，面ABD，面ACD；棱AD；平面角∠BDC．

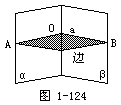
2．如图1-124，平面AOB⊥a，平面AOB与平面α、β的交

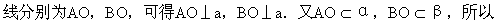
∠AOB是二面角α-a-β的平面角．

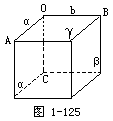
3．如图1-125，二面角α-c-β，二面角β-b-γ，二面角α-a-γ的平面角分别为∠AOB，∠AOC，∠BOC，都是90°．

4．已知：如图1-126，二面角α-AB-β为30°，P∈α，P到平面β的距离为10cm．

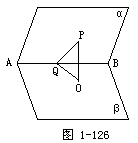
求P到AB的距离．

解：在β内作点P的射影O，过点P作PQ⊥AB于Q，连结OQ，根据三垂线定理，可得OQ⊥AB．

∴∠PQO为二面角α-AB-β的平面角，即∠PQO＝3O°．

∵PO＝10cm，

∴PQ＝20cm．

即P到AB的距离为20cm．

小结：从上面四题练习，我们可以总结三种作二面角的平面角的一般方法．

1．定义法：以二面角的棱上某一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角即二面角的平面角(如练习1，3)．

2．应用三垂线(逆)定理法：在二面角α-l-β的面α上取一点A，作AB⊥β于B，BC⊥l于C，则∠ACB即为α-l-β的平面角(如练习4)．

3．作垂面法：作棱的垂面，则它和二面角的两个面的交线所成的角就是二面角的平面角(如练习2)．