
(二)两个平面垂直的性质
师:今天我们接着研究两个平面垂直的性质.
两个平面垂直的性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面.
已知:平面α⊥β,α∩β=CD,AB 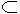 α且AB⊥CD于B.
α且AB⊥CD于B.
求证:AB⊥β.
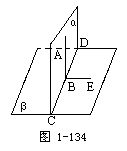
证明:在平面β内引直线BE⊥CD,则∠ABE是二面角α-CD-β的平面角.
∵α⊥β,∴AB⊥BE.
又∵AB⊥CD,∴AB⊥β.
师:从性质定理可以得出,把面面垂直的问题转化为线面垂直的问题.
例1 如果两个平面互相垂直,那么经过第一个平面内的一点垂直于第二个平面的直线,在第一个平面内.
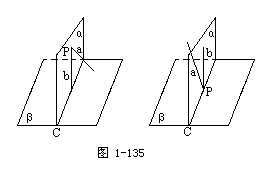
已知:α⊥β,P∈α,P∈a,a⊥β.
求证:a 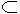 α.
α.
师提示:要证明a 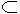 α,一般用反证法,即否定结论→推出矛盾→肯定结论.下面请同学们写出它的证明过程.
α,一般用反证法,即否定结论→推出矛盾→肯定结论.下面请同学们写出它的证明过程.
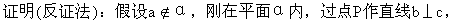
其中c为α与β的交线.
∵α⊥β,∴b⊥β.
又∵P∈α,P∈a,a⊥β,
这与“过一点P有且只有一条直线与已知平面垂直”矛盾.
∴a 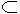 α.
α.
师:现在我们来看课本P.44的证明,这种方法叫同一法.什么是同一法呢?(幻灯显示)
一个命题,如果它的题设和结论所指的事物都是唯一的,那么原命题和它的逆命题中,只要有一个成立,另一个就一定成立,这个道理叫做同一法则.在符合同一法则的前提下,代替证明原命题而证明它的逆命题成立的一种方法叫做同一法.
同一法的一般步骤是什么?(幻灯显示)
1.不从已知条件入手,而另作图形使它具有求证的结论中所提的特性;
2.证明所作的图形的特性,与已知条件符合;
3.因为已知条件和求证的结论所指的事物都是唯一的,从而推出所作的图形与已知条件要求的是一个东西,由此断定原命题成立.
证明(同一法):设α∩β=c,过点P在平面α内作直线b⊥c,根据上面的定理有b⊥β.
因为经过一点只能有一条直线与平面β垂直,所以直线a应与直线b重合.
即a 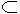 α.
α.
师:比较反证法与同一法,我们可以知道:凡可用同一法证明的命题也可用反证法来证;反证法可适用于各种命题,同一法只适用于符合同一法则的命题.
另外,例1的结论也可作为两个平面垂直的另一个性质,可直接应用.
下面请同学们一齐完成例2.
本课题安排2课时.本节课为第二课时,主要讲解两个平面垂直的性质及异面直线上两点间的距离公式.
3.教学疑点:
(1)弄清反证法与同一法的联系与区别.
(2)正确理解、应用异面直线上两点间的距离公式:EF=
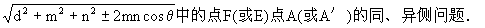
2.教学难点:异面直线上两点间距离公式的应用.
1.教学重点:掌握两个平面垂直的性质;会运用异面直线上两点间的距离公式.
(二)能力训练点
1.弄清反证法与同一法之间的关系,并会应用同一法证题,进一步培养学生的逻辑思维能力.
2.掌握两个平面垂直的性质定理,理解面面垂直问题可能化为线面垂直的问题.
3.异面直线上任意两点间的距离公式不仅可用于求其值,还可以证明两条异面直线的距离是异面直线上两点的距离中最小的.另外,还可解决分别在二面角的面内两点的距离问题.
(一)知识教学点
1.两个平面垂直的性质定理.
2.异面直线上两点间的距离公式.
22. 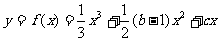
(1)在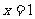 、
、 处取得极值,求
处取得极值,求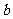 、
、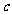
(2)若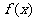 在(
在( ,
,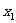 ),(
),(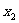 ,
, )
) (
(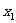 ,
,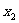 )
) 且
且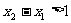 ,求证:
,求证: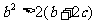
(3)在(2)的条件下, ,试比较,
,试比较,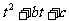 与
与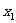 的大小关系。
的大小关系。
21. 等差数列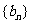 中,
中,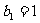 ,
,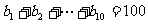
(1)求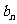 通项;
通项;
(2)若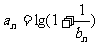 记
记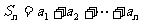 ,试比较
,试比较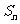 与
与 的大小关系。
的大小关系。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com