
2.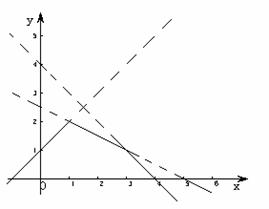 x为何值时,y最大?最大值是多少?
x为何值时,y最大?最大值是多少?
解:1.易得A(1, 2) B(3, 1)
∴y与x的函数关系是:
|
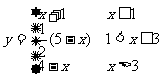

1.求y与x的函数关系,并画出函数的图象。
值和最小值。
解:∵f (x)的定义域为[1, 4] ∴g(x)的定义域为[1, 2]
∵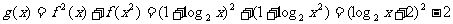
∵1≤x≤2 ∴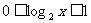
∴当x = 1时, g (x)max = 2 ;当x = 2时, g (x)min = 7
3.∵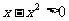 在区间内
在区间内 在
在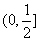 上递增,在
上递增,在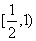 上递减。
上递减。
当0<a<1时, 函数在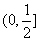 上是减函数, 在
上是减函数, 在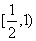 是增函数。
是增函数。
当a>1时, 函数在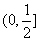 上是增函数, 在
上是增函数, 在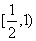 是减函数。
是减函数。
解:1.定义域: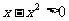 得:
得: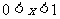
2.∵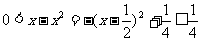
∴当0<a<1时,
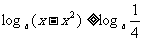 函数的值域为
函数的值域为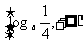
当a>1时,
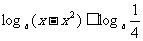 函数的值域为
函数的值域为
A作x轴的垂线,垂足为E,过点B作y轴的垂线,交EA于C,若C
恰好在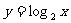 函数的图象上,试求A、B、C三点的坐标。
函数的图象上,试求A、B、C三点的坐标。
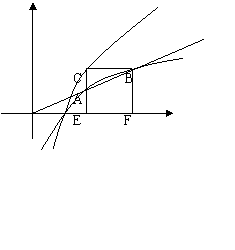 解:设A(x1 ,
解:设A(x1 , 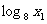 ) , B(x2 ,
) , B(x2 , 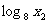 ) , 则C(x1 ,
) , 则C(x1 , 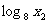 )
)
∵C在函数的图象上 ∴ 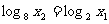
即: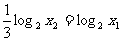 ∴ x2 = x13
∴ x2 = x13
又: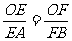 即:
即: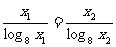 ∴
∴
∴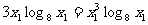 由x1>1
, ∴log 8x1¹1 从而有:3x1=x13
由x1>1
, ∴log 8x1¹1 从而有:3x1=x13
∴
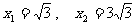
∴A、B、C三点的坐标分别为: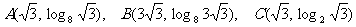
P.46中习题六9、10(2)、11、12.
(四)练习
在60°二面角的枝上,有两个点A、B,AC、BD分别是在这个二面角的两个面内垂直于AB的线段.已知:AB=4cm,AC=6cm,BD=8cm,利用异面直线上两点距离公式求CD.(P.45中练习3)

∴AC与BD是异面直线.
∵AB⊥AC交于点A,AB⊥BD交于点B,
∴AB是AC、BD的公垂线,AC、BC所成角是60°.
已知AB=4cm,AC=6cm,BD=8cm.
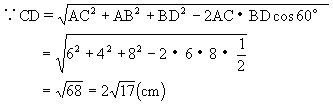
师点评:根据二面角的平面角来求异面直线上两点间的距离时,应用异面直线上两点间的距离公式一定要注意cosθ前正负号的选择(当θ≤90°时取“-”号).
(三)异面直线上两点间的距离
例2 已知两条异面直线a、b所成的角为θ,它们的公垂线段AA'的长度为d.在直线a、b上分别取点E、F,设,A'E=m,AF=n,求EF.
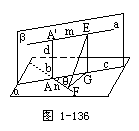
解:设经过b与a平行的平面为α,经过a和AA'的平面为β,α∩β=c,则c∥a,因而b、c所成的角等于θ,且AA'⊥C.
又∵AA'⊥b,
∴AA'⊥α.
根据两个平面垂直的判定定理,β⊥α,在平面β内作EG⊥C,则EG=AA'.并且根据两个平面垂直的性质定理,EG⊥α.连结FG,则EG⊥FG.在Rt△FEG中.
EF2=EG2+FG2
∵AG=m,
∴在△AFG中.
FG2=m2+n2-2mncosθ.
又∵EG2=d2
∴EF2=dw+m2+n2-2mncosθ.
如果点F(或E)在点A(或A')的另一侧,则EF2=d2+m2+n2+2mncosθ.
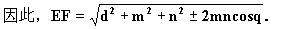
师:例2不仅求出两条异面直线上任意两点间的距离公式,还解决了下面的三个问题:
(1)证明了两条异面直线公垂线的存在性.
(2)证明两条异面直线的距离是异面直线上两点的距离最小的.
∵AA'=EG,且AA',EG是平面α的垂线,而EF是斜线,
∴AA'<EF.
如在实际中,两条交叉的高压电线如果放电时,火花正是通过它们的最短距离.
(3)也可以解决分别在二面角的面内两点的距离问题,请看下面练习.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com