
(三)德育渗透点
1.理解并掌握两个平面垂直定义的过程是培养学生从一般到特殊的思维方法的过程.
2.让学生认识到掌握两个平面垂直的判定定理是人类生产实践的需要,并且应用于实践,进一步培养学生理论与实践相结合的观点.
(二)能力训练点
1.应用演绎的数学方法理解并掌握两个平面垂直的定义.
2.掌握两个平面垂直的判定定理的证明过程,培养学生严格的逻辑推理,增强学生分析、解决问题的能力.
3.利用转化的方法掌握和应用两个平面垂直的判定定理.
(一)知识教学点
1.两个平面垂直的定义、画法.
2.两个平面垂直的判定定理.
6.(a1+a2+…+an)/n; 7.5400.
8.依题意,每天获利y元与每件销售价x元的函数关系为
y=(x-50)·p
=[105(x-5)]/[(x-4)2](50≤x≤80).
将函数解析式变形为
y=…=-106((1/x-4)-(1/20))2+2500.
∵50≤x≤80,∴(1/40)≤(1/x-40)≤(1/10).
∴当(1/x-40)=(1/20),即x=60时,ymax=2500.?
9.(1)由图2-7,得
P=|x-10|(0≤x≤20);
由图2-8,得Q=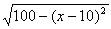 (0≤x≤20).
∴y=P·Q·100=100|x-10|·
(0≤x≤20).
∴y=P·Q·100=100|x-10|·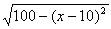 ?(1≤x≤20,x∈N).
(2)y=100|x-10|
?(1≤x≤20,x∈N).
(2)y=100|x-10|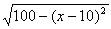 ≤100·(|x-10|2+[
≤100·(|x-10|2+[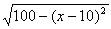 ]2/2)
=500.
当且仅当|x-10|=
]2/2)
=500.
当且仅当|x-10|=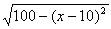 ,即x=10±5
,即x=10±5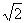 ≈17或3时,上式等号成立.
故第3天或第17天的销售收入最高,此食品每件定价7元最好.
10.(1)设此合金中含A金属x克,含B金属y克,根据题意得
≈17或3时,上式等号成立.
故第3天或第17天的销售收入最高,此食品每件定价7元最好.
10.(1)设此合金中含A金属x克,含B金属y克,根据题意得
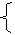 |
x+y=400, |
|
(x/d)+y/(7.2)=50. |
解得x=(40d)/(d-7.2),y=(360(d-8)/(d-7.2)(8.8<d<9). (2)∵x=40d/(d-7.2)=40(1+(7.2/(d-7.2))在(8.8,9)上是减函数,y=(360(d-8)/d-7.2)=360(1-[0.8/(d-7.2)])在(8.8,9)上是增函数, ∴200<x<220,180<y<200.
6.(a1+a2+…+an)/n; 7.5400.
8.依题意,每天获利y元与每件销售价x元的函数关系为
y=(x-50)·p
=[105(x-5)]/[(x-4)2](50≤x≤80).
将函数解析式变形为
y=…=-106((1/x-4)-(1/20))2+2500.
∵50≤x≤80,∴(1/40)≤(1/x-40)≤(1/10).
∴当(1/x-40)=(1/20),即x=60时,ymax=2500.?
9.(1)由图2-7,得
P=|x-10|(0≤x≤20);
由图2-8,得Q=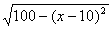 (0≤x≤20).
∴y=P·Q·100=100|x-10|·
(0≤x≤20).
∴y=P·Q·100=100|x-10|·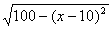 ?(1≤x≤20,x∈N).
(2)y=100|x-10|
?(1≤x≤20,x∈N).
(2)y=100|x-10|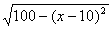 ≤100·(|x-10|2+[
≤100·(|x-10|2+[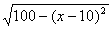 ]2/2)
=500.
当且仅当|x-10|=
]2/2)
=500.
当且仅当|x-10|=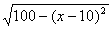 ,即x=10±5
,即x=10±5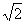 ≈17或3时,上式等号成立.
故第3天或第17天的销售收入最高,此食品每件定价7元最好.
10.(1)设此合金中含A金属x克,含B金属y克,根据题意得
≈17或3时,上式等号成立.
故第3天或第17天的销售收入最高,此食品每件定价7元最好.
10.(1)设此合金中含A金属x克,含B金属y克,根据题意得
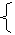 |
x+y=400, |
|
(x/d)+y/(7.2)=50. |
解得x=(40d)/(d-7.2),y=(360(d-8)/(d-7.2)(8.8<d<9). (2)∵x=40d/(d-7.2)=40(1+(7.2/(d-7.2))在(8.8,9)上是减函数,y=(360(d-8)/d-7.2)=360(1-[0.8/(d-7.2)])在(8.8,9)上是增函数, ∴200<x<220,180<y<200.
6.在测量某物理量的过程中,因仪器和观察的误差,使得几次测量分别得到a1,a2,…,an共n个数据.我们规定所测量物理量的“最佳近似值”a是这样一个量:与其它近似值比较,a与各数据的差的平方和最小.依此规定,从a1,a2,…,an推出的a=_________.
7.做一个容积为4m3的圆柱形油桶,若两底材料600元/m2,侧面材料300元/m2,则最节省的材料费约为_________元(取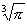 =1.5).
8.某商品进货价每件50元,销售价每件x元,据市场调查,当50≤x≤80时,每天销售的件数为p=(105/(x-40)2).若想每天获得利润最大,销售价应确定为多少元?
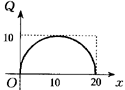
9.某食品专卖店为了弄清某食品的市场行情,进行了为期20天的调查,对每天的价格和销售量作好记录,将结果描在坐标平面上,可近似地得到价格(每件P元)与天数的关系如图2-7所示,销售量Q(百件)与天数的关系如图2-8(半圆)所示.
=1.5).
8.某商品进货价每件50元,销售价每件x元,据市场调查,当50≤x≤80时,每天销售的件数为p=(105/(x-40)2).若想每天获得利润最大,销售价应确定为多少元?
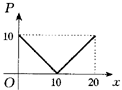
9.某食品专卖店为了弄清某食品的市场行情,进行了为期20天的调查,对每天的价格和销售量作好记录,将结果描在坐标平面上,可近似地得到价格(每件P元)与天数的关系如图2-7所示,销售量Q(百件)与天数的关系如图2-8(半圆)所示.
 |
 |
|
图2-7 |
图2-8 |
(1)求销售收入y(元)与天数(x)的函数关系式; (2)销售收入最高的大约是哪一天?此食品每件定价多少元最好?(精确到1元) 10.华宇航天有限公司试制一种仅由金属A和金属B合成的合金,现已试制出这种合金400克,它的体积为50立方厘米.已知金属A的比重d小于每立方厘米9克,大于每立方厘米8.8克;金属B的比重约为每立方厘米7.2克. (1)试用d分别表示出此合金中金属A、金属B克数的函数关系式; (2)求已试制的合金中金属A、金属B的克数在什么范围内取值.
8.(1)若函数y=f(x)满足f(a+x)=f(b-x),则y=f(x)的图象关于直线x=(a+b)/2对称; (2)若函数y=f(x)满足f(a+x)=-f(b-x),则y=f(x)的图象关于点((a+b)/2,0)中心对称. 9.已知函数f(x)的定义域为R,且对一切实数x满足f(2+x)=f(2-x),f(7+x)=f(7-x). (1)若f(5)=9,求f(-5)的值; (2)已知x∈[2,7]时,f(x)=(x-2)2.求当x∈[16,20]时函数g(x)=2x-f(x)的表达式,并求出g(x)的最大值和最小值. 10.设函数
f1(x)=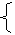 |
0 (x=0), |
|
-(1/2)x (4k-1≤|x|<2×4k-1,k∈Z), |
|
|
2x (2×4k-1≤|x|≤4k,k∈Z). |
(1)求f1(x)的定义域; (2)y=f1(x)的图象绕坐标原点旋转π/2后,得到y=f2(x)的图象,试求y=f2(x)的解析式; (3)对定义在实数集R上的函数f(x),如果y=f(x)的图象绕坐标原点旋转π/2后不变,试证明方程f(x)=x恰好有一个解.
17. 已知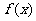 的值域为
的值域为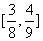 ,求
,求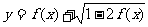 的值域。
的值域。
16. 设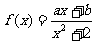 的值域为
的值域为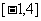 ,求
,求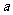 、
、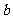 的值。
的值。
15. 求函数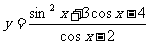 的值域。
的值域。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com