1．某产品的总成本 y万元与产量 x台之间的函数关系式是 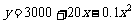　xÎ(0,240)，若每台产品的售价为25万元，则生产者不亏本的最低产量为多少？

解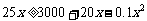：　　　 即：　 　　

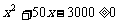
∴x≥150　 (x≤-120　 舍去)　　　 即：最低产量为150台　　　　　　　　

P．46中习题六．6、7、8、10(1)，

(五)总结

本节课我们讲解了两个平面垂直的定义、画法及判定方法．判定方法有两种，一是利用定义，二是利用判定定理．如何应用两个平面垂直的判定定理，把面面垂直的问题转化为线面垂直的问题是本节课学习的关键．

(四)练习

例：⊙O在平面α内，AB是⊙O的直径，PA⊥α，C为圆周上不同于A、B的任意一点．

求证：平面PAC⊥平面PBC．

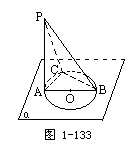
证明：在θO内．

∵AB为θO的直径，

∴BC⊥AC．

又PA⊥BC，

∴BC⊥平面PAC．

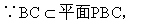
∴平面PAC⊥平面PBC．

(三)两个平面垂直的判定

师：判定两个平面互相垂直，除了定义外，还有下面的判定定理．

两个平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直．

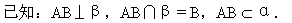
求证：α⊥β．

师提示：要证明两个平面互相垂直，只有根据两个平面互相垂直的定义，证明由它们组成的二面角是直二面角，因此必须作出它的一个平面角，并证明这个平面角是直角．如何作平面角呢？根据平面角的定义，可以作BE⊥CD，使∠ABE为二面角α-CD-β的平面角．

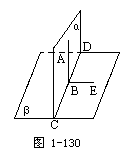
让学生独自写出证明过程．

证明：设a∩β=CD，则B∈CD．

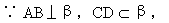
∴AB⊥CD．

在平面β内过点B作直线BE⊥CD，则∠ABE是二面角α-CD-β的平面角，又AB⊥BE，即二面角α-CD-β是直二面角．

∴α⊥β．

师：两个平面垂直的判定定理，不仅是判定两个平面互相垂直的依据，而且是找出垂直于一个平面的另一个平面的依据．如：建筑工人在砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和水平面垂直(图见课本P.43中图1-49)，实际上，就是依据这个原理．

另外，这个定理说明要证明面面垂直，实质上是转化为线面垂直来证明．下面我们来做一道练习．

练习：(P.45中练习2)

如图1-131，检查工件的相邻两个面是否垂直时，只要用曲尺的一边紧靠在工件的一个面上，另一边在工件的另一个面上转动一下，观察尺边是否和这个面密合就可以了．为什么？如果不转动呢？

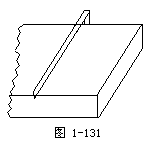
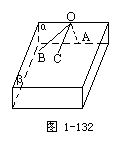
如果不转动，只能确定两条直线OA⊥OB，无法确定OA⊥β，从而无法确定α⊥β．

(二)两个平面垂直的定义、画法

师：两个平面垂直是两个平面相交的特殊情况，日常我们见到的墙面和地面、以及一个长方体中，相邻的两个面都是互相垂直的．那么，什么是两个平面互相垂直呢？

生：两个平面相交，如果所成的二面角是直二面角，就说这两个平面互相垂直．

师：回答得很好．这个定义与平面几何里的两条直线互相垂直的定义相类似，也是用它们所成的角是直角来定义．知道了两个平面互相垂直的概念．如何画它们呢？

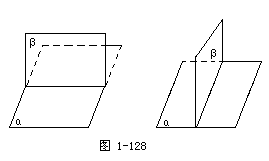
生：如图1-128，把直立平面的竖边画成和水平平面的横边垂直．记作α⊥β．

练习：(P.45中练习1)

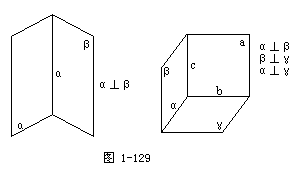
画互相垂直的两个平面、两两垂直的三个平面．

如图1-129．

本课题安排2课时．本节课为第一课时：主要讲解两个平面垂直的判定．

2．教学难点：掌握两个平面垂直的判定及应用．

1．教学重点：掌握两个平面垂直的判定．