
1、已知集合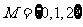 ,
,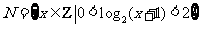 ,则
,则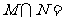
A. {1,2} B{1} C{2} D{3}
这种方式一般用于列举几个典型事例之后,归纳出几个事例的共性,这共性就与论点紧密联系起来了。如: 一个人要具有内在美,必须经过艰苦的磨练。柳敬亭说书能独领风骚,离不开长期的“简练揣摩”;宋濂能成为明朝鸿儒,靠的是遍访名师,刻苦学习;张海迪能成为一个合格的医生,付出了多于常人无数倍的努力。这些人的成才历程,都充分证明了内在美的获取,不是轻而易举的,而是要经过长期不懈的努力,须付出“血和肉”的代价,而不是“高高浮在潮的上头”就能得到的。
22.(14分)正项数列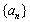 和
和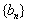 满足:
满足: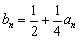 ,
,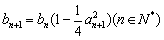 ,
,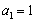
(1)求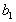 ,
,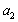 ;
;
(2)求数列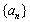 和
和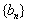 的通项公式;
的通项公式;
(3)设 ,求
,求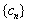 的前
的前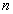 项和
项和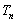 .
.
21.(12分)已知正三棱柱ABC-A1B1C1的每条棱长均为2,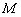 为棱A1C1上的动点,
为棱A1C1上的动点,
(1)当M在何处时,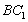 ∥平面MB1A,并证明之;
∥平面MB1A,并证明之;
(2)在(1)条件下,求平面MB1A与平面ABC所成的二面角的大小;
(3)在(1)条件下,求AB与平面MB1A所成角的大小.
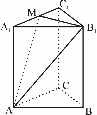
20.(12分)设函数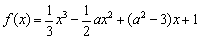
(1)若函数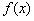 在
在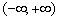 上是增函数,求实数
上是增函数,求实数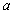 的取值范围;
的取值范围;
(2)若函数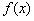 的单调递减区间为
的单调递减区间为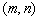 ,且
,且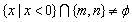 .求实数
.求实数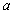 的取值范围.
的取值范围.
19.(12分)今年某地旱情严重,准备用炮弹射击的方法实行人工降雨。已知只有5发炮弹,对同一片积云进行射击,命中积云一次只能使云层中的水分子凝集,命中积云两次才能降雨,如果已降雨或炮弹打完,则停止射击。每次射击是相互独立的,且每次命中的概率均为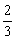 .
.
(1)求第三次射击后才能降雨的概率;
(2)求这次人工降雨成功的可能性有多大?
18.(12分)设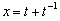 ,
,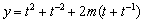 ,其中
,其中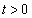 ,
,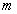 为常数.
为常数.
(1)将 表示成
表示成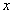 的函数
的函数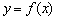 ,并求其定义域;
,并求其定义域;
(2)设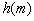 是函数
是函数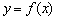 的最小值,求
的最小值,求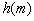 的表达式.
的表达式.
17.(12分)
(1)等差数列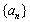 中,
中,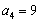 ,
, ,
,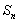 为其前
为其前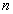 项和,求满足
项和,求满足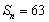 的
的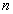 的值;
的值;
(2)等比数列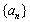 中,
中,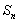 是其前
是其前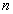 项和,
项和,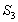 是
是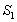 和
和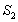 的等差中项,求数列
的等差中项,求数列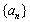 的公比
的公比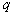 的值.
的值.
16.下列命题中:
①若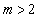 ,则不等式
,则不等式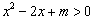 的解集为R;
的解集为R;
②“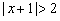 ”是“
”是“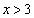 ”的必要不充分条件;
”的必要不充分条件;
③在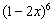 的展开式中
的展开式中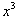 的系数是
的系数是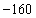 ;
;
④设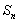 为
为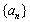 的前
的前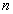 项和,若
项和,若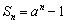 (
( ,
,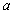 为常数),则
为常数),则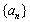 是等比数列或等差数列.
是等比数列或等差数列.
其中真命题为________(填上你认为正确命题的所有序号).
15.已知一个四面体的一条棱长为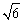 ,其余棱长均为2,则此四面体的外接球半径为_______.
,其余棱长均为2,则此四面体的外接球半径为_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com