
6.利用导数求函数的最值步骤:
由上面函数 的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.
的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.
设函数 在
在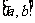 上连续,在
上连续,在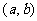 内可导,则求
内可导,则求 在
在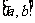 上的最大值与最小值的步骤如下:
上的最大值与最小值的步骤如下: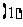 求
求 在
在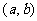 内的极值;
内的极值;
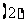 将
将 的各极值与
的各极值与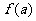 、
、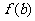 比较得出函数
比较得出函数 在
在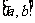 上的最值
上的最值 p
p
5.函数的最大值和最小值: 一般地,在闭区间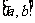 上连续的函数
上连续的函数 在
在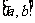 上必有最大值与最小值.
上必有最大值与最小值.
 利用导数研究多项式函数单调性的一般步骤:
利用导数研究多项式函数单调性的一般步骤:
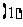 求
求 ;
;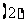 确定
确定 在
在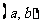 内符号;
内符号;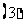 若
若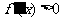 在
在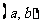 上恒成立,则
上恒成立,则 在
在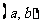 上是增函数;若
上是增函数;若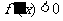 在
在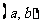 上恒成立,则
上恒成立,则 在
在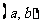 上是减函数
上是减函数
①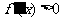

 为增函数(
为增函数(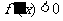

 为减函数).
为减函数).
② 在区间
在区间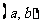 上是增函数
上是增函数
 ≥
≥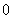 在
在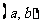 上恒成立;
上恒成立;
 在区间
在区间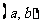 上为减函数
上为减函数
 ≤
≤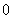 在
在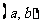 上恒成立.
上恒成立.
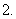 极大值: 一般地,设函数
极大值: 一般地,设函数 在点
在点 附近有定义,如果对
附近有定义,如果对 附近的所有的点,都有
附近的所有的点,都有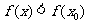 ,就说
,就说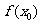 是函数
是函数 的一个极大值,记作
的一个极大值,记作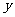 极大值
极大值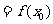 ,
, 是极大值点.
是极大值点.
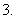 极小值:一般地,设函数
极小值:一般地,设函数 在
在 附近有定义,如果对
附近有定义,如果对 附近的所有的点,都有
附近的所有的点,都有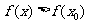 就说
就说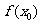 是函数
是函数 的一个极小值,记作
的一个极小值,记作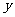 极小值
极小值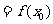 ,
, 是极小值点。
是极小值点。
4.求可导函数 的极值的步骤:
的极值的步骤:
 确定函数的定义区间,求导数
确定函数的定义区间,求导数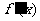
 求方程
求方程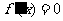 的根
的根
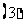 用函数的导数为
用函数的导数为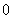 的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查
的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查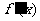 在方程根左右的值的符号,如果左正右负,那么
在方程根左右的值的符号,如果左正右负,那么 在这个根处取得极大值;如果左负右正,那么
在这个根处取得极大值;如果左负右正,那么 在这个根处取得极小值;如果左右不改变符号,那么
在这个根处取得极小值;如果左右不改变符号,那么 在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 .
在这个根处无极值.如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 .
考纲点击: 理解可导函数的单调性与其导数的关系;
理解可导函数的单调性与其导数的关系;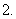 了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);
了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);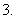 会求一些实际问题(一般指单峰函数)的最大值和最小值.
会求一些实际问题(一般指单峰函数)的最大值和最小值.
热点提示:
导数的应用已成为高考必考点,重点考查利用导数研究函数的单调性,求单调区间、极值、最值,以及利用导数解决生活中优化问题,可以与解析几何、不等式、平面向量等知识交汇命题。多以解答题出现,属中高档题。
12.如图25(1)、25(2)、25(3)中,点E、D分别是正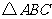 、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE = CD,DB交AE于P点.
、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE = CD,DB交AE于P点.
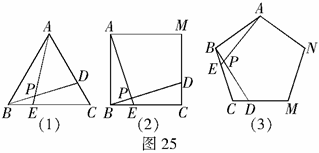
(1)图25(1)中,∠APD的度数为________;
(2)图25(2)中,∠APD的度数为________,图25(3)中,∠APD的度数为________;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况.若能,写出推广问题和结论;若不能,请说明理由.
11.如图24,已知正方形ABCD中,E为BC上一点,将正方形折叠起来,使点A和点E重合,折痕为MN,若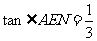 ,
,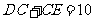 .
.
(1)求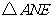 的面积.
的面积.
(2)求 的值.
的值.
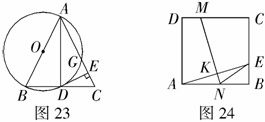
10.如图23,以等腰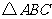 的一腰AB为直径的
的一腰AB为直径的 交BC于点D,交AC于点G,连结AD,并过点D作DE⊥AC,垂足为E.DE是
交BC于点D,交AC于点G,连结AD,并过点D作DE⊥AC,垂足为E.DE是 的切线吗?请说明理由.
的切线吗?请说明理由.
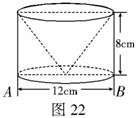
8.如图21,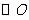 的直径AD过弦EF的中点G,
的直径AD过弦EF的中点G,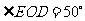 ,则∠DAF等于( )
,则∠DAF等于( )
(A)100° (B)50°
(C)40° (D)25°
 9.如图22,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB=12cm,高BC=8cm,求这个零件的全面积.(结果保留π)
9.如图22,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥体而得到的,其底面直径AB=12cm,高BC=8cm,求这个零件的全面积.(结果保留π)
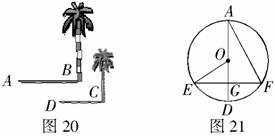
7.如图20,平面上两颗不同高度、笔直的小树,同一时刻在太阳光线照射下形成的影子分别是AB、DC,则 ( )
(A)四边形ABCD是平行四边形
(B)四边形ABCD是梯形
(C)线段AB与线段CD相交
(D)以上三个选项均有可能
6.不能判定四边形ABCD为平行四边形的题设是( )
(A)AB平行且等于CD (B)∠A=∠C,∠B=∠D
(C)AB=AD,BC=CD (D)AB=CD,AD=BC
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com