主要考点：

1．常识：温度、压强对物质溶解度的影响；混合物分离的常用方法

①　　 一般固体物质受压强影响不大，可以忽略不计。而绝大部分固体随着温度的升高，其溶解度也逐渐升高(如：硝酸钾等)；少数固体随着温度的升高，其溶解度变化不大(如：氯化钠等)；极少数固体随着温度的升高，其溶解度反而降低的(如：氢氧化钙等)。

气体物质的溶解度随着温度的升高而降低，随着压强的升高而升高。

②　　 混合物分离的常用方法主要包括：过滤、蒸发、结晶

过滤法用于分离可溶物与不溶物组成的混合物，可溶物形成滤液，不溶物形成滤渣而遗留在滤纸上；

结晶法用于分离其溶解度受温度影响有差异的可溶物混合物，主要包括降温结晶法及蒸发结晶法

降温结晶法用于提取受温度影响比较大的物质(即陡升型物质)，如硝酸钾中含有少量的氯化钠；

蒸发结晶法用于提取受温度影响不大的物质(即缓升型物质)，如氯化钠中含有少量的硝酸钾；

　　　　　　　　　　　 《教学与测试》 　P58 　　6、7

　　　　　　　　　 设 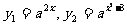，其中 a > 0，a ¹ 1，

问：x为何值时有1° y₁ = y₂ 　2° y₁ < y₂

　　　　　 解：1．由于指数函数是单调函数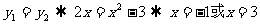，∴　 　　　　　　　　　　2．当 0 < a < 1，由 y₁ < y₂ ，得 2x > x² -3 ，解得 -1 < x < 3

　　　　　　　　　　　　 当 　a > 1，由 y₁ < y₂ ，得 2x < x² -3 ，解得 x < -1 或 x > 3

3．图象如图所示：

　　　　　　　　　　　　 当 k < 0时，直线 y = k与函数 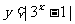图象无交点　　　 ∴方程无解。

　　　　　　　　　　　　 当 k = 0或 k ≥ 1时，直线 y = k与函数 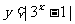图象有一个交点　　　 ∴方程有一解。

　　　　　　　　　　　　 当 0 < k < 1时，直线 y = k与函数 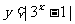图象有两个交点　　　

∴方程有两解。

2．画出函数 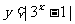　的图象，并利用图象回答：k 为何值时，方程　 无解？有一解？有两解？

　　　　　 解：1．定义域：x ¹ 0

　　　　　　　　　　　 　若 f (x)为奇函数，则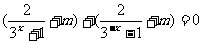 　

　　　　　　　　　　　　 ∴

1．已知 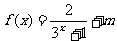　是奇函数，求常数 m 的值。

　　　　　　　　　　 求函数 　的值域和单调区间。

　　　　　　 解：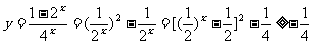　

∴函数的值域为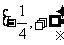

　　　　　　　　　　 ∵设 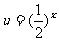,　 它在 　上单调递减，

而二次函数 在 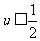　时是减函数，在 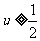时是增函数令 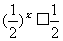，则 x ≥ 1　　　　　 　令 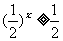，则 x ≤ 1 　

　 　　　　　　　　　∴函数 　在 上是增函数，在上是减函数。

　　　　　　　　　　 1° 求证： f (x) 是奇函数。

　　　　　　　　　　 2° 若 f (-3) = a，试用 a 表示 f (24)　

　　　　　　　　　　 3° 如果 x > 0 时，f (x) > 0 且 f (1) < 0，试求 f (x) 在区间[-2，6]上的

最大值与最小值。

　　　 　　　解：1° 令 x = y = 0　 得 f (0) = 0，再令 y = - x　 得　 f (0) = f (x) + f (- x),　　　　　

∴f (x) = f (- x)　　 ∴f (x)为奇函数

　　　　　　　　　　 2° 由 f (-3) = a　 得 f (3) = - f(-3) = -a，

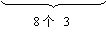f (24) = f ( 3 + 3 + …… + 3) = 8 f (3) = - f (3)

　　　　　　　　　　 3° 设　 x ₁ < x₂ ，则 f (x₂) = f (x ₁ + x₂ - x ₁) = f (x ₁) + f (x₂ - x ₁) < f (x ₁)，

( ∵ x₂ - x ₁ > 0 ,　 f ( x₂ - x ₁) < 0 )

　　　　　　　　　　　　 　∴f (x) 在区间[-2，6]上是减函数。

　　　　　　　　　　　　 ∴f (x) _max = f (-2) = -f (2) = -2f (1) = 1

　　　　　　　　　　　　 　　f (x) _min 　= f (6) = 6 f (1) = -3

　　　　　　　　　　 已知函数　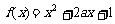 在区间[-1，2]上的最大值是4，求 　a的值。

　　 　　　　解：抛物线对称轴为 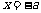　,　 区间[-1，2]中点为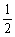

　　　　　　　　　 1° 当 2≥-a ,　 即 a≤-2时，由题设：f (-1) = 4,　 即 1 - 2a +1 = 4,　 a = -1

　　　　　　 　　　　　(不合)

　　　　　　　　　 2° 当 ,　 即 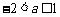时，由题设：f (-1) = 4,　 即　 a = -1 　　　　　　　　　　　

　　　　　　　　　 3° 当 ,　 即时，由题设：f (2) = 4,　 即 4 + 4a +1 = 4,　

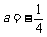
　　　　　　 　　　4° 当 -a<-1, 　即 a>1时，由题设：f (2) = 4,　 即 4 + 4a +1 = 4,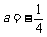　 　

　　　　　　　　　　　 (不合)

　　　　　　　　　 注：若是已知最小值，此种分类同样适用，也可分 -a 在 　　　

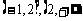　　　　　　　　　　　　　 三个区间。但本题亦可将1°、2°和3°、4°分别合并成

两个区间讨论。

P．38-39中习题五4、5、6、7、8．