
6.若函数 的反函数是
的反函数是 ,
, ,则
,则 等于 ( )
等于 ( )
A.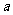 B.
B. C.
C. D.
D.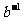

5.设函数 ,则
,则 的定义域为 ( )
的定义域为 ( )
A. B.
B. C.
C.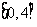 D.
D.

4.与函数y=f(x)的反函数图象关于原点对称的图象所对应的函数是 ( )
A.y=-f(x)
B.y= f-1(x) C.y =-f-1(x) D.y =-f-1(-x)

3.若f(x-1)=
x2-2x+3 (x ≤1),则f-1(4)等于 ( )
A. B.1-
B.1- C.-
C.- D.
D. -2
-2 
1 .设函数f(x)=1-
.设函数f(x)=1- (-1≤x≤0),则函数y=f-1(x)的图象是 ( )
(-1≤x≤0),则函数y=f-1(x)的图象是 ( )
A.
y B. y 1 C. y D.
y 1
1
x 1
O
x
-1
-1
-1 O x
O
1 x
2.函数y=1- (x≥1)的反函数是 ( )
(x≥1)的反函数是 ( )
A.y=(x-1)2+1,x∈R B.y=(x-1)2-1,x∈R
C.y=(x-1)2+1,x≤1 D.y=(x-1)2-1,x≤1
3. 3 一次函数的应用
2010年中考数学代数公式、定理汇编(九):第九章 二次函数
1 二次函数及其图像
11 二次函数
我们把函数y=ax²+bx+c(a,b,c为常数,且a不等于0)叫做二次函数
12 函数y=ax²(a不等于0)的图像和性质
用表里各组对应值作为点的坐标,进行描点,然后用光滑的曲线把它们顺次联结起来,就得到函数y=x²的图象这个图象叫做抛物线函数y=x²的图像,以后简称为抛物线y=x²这条抛物线是关于y轴成对称的我们把y轴叫做抛物线y=x²的对称轴对称轴和抛物线的焦点,叫做抛物线的顶点
13 函数y=ax²+bx+c(a不等于0)的图像和性质
抛物线y=ax²+bx+c的顶点坐标是(-b/2a,4ac-b²/4a),对称轴方程是x=-b/2a,当a〉0时,抛物线的开口向上,并且向上无限延伸;当a〈0时,抛物线的开口向下,并且向下无限延伸
当a〉0时,二次函数y=ax²+bx+c在x〈-b/2a时是递减的,在x〉-b/2a时是递增的;在x=-b/2a处取得y最小=4ac-b²/4a当a〈0时,二次函数y=ax²+bx+c在x〈-b/2a时是递减的;在x=-不/2a处取得y最大=4ac-b²/4a
2 根据已知条件求二次函数
21 根据已知条件确定二次函数
22 二次函数的最大值或最小值
23 一元二次方程的图像解法
2010年中考数学几何公式、定理汇编(一)
1 过两点有且只有一条直线
2 两点之间线段最短
3 同角或等角的补角相等
4 同角或等角的余角相等
5 过一点有且只有一条直线和已知直线垂直
6 直线外一点与直线上各点连接的所有线段中,垂线段最短
7 平行公理 经过直线外一点,有且只有一条直线与这条直线平行
8 如果两条直线都和第三条直线平行,这两条直线也互相平行
9 同位角相等,两直线平行
10 内错角相等,两直线平行
11 同旁内角互补,两直线平行
12两直线平行,同位角相等
13 两直线平行,内错角相等
14 两直线平行,同旁内角互补
15 定理 三角形两边的和大于第三边
16 推论 三角形两边的差小于第三边
17 三角形内角和定理 三角形三个内角的和等于180°
18 推论1 直角三角形的两个锐角互余
19 推论2 三角形的一个外角等于和它不相邻的两个内角的和
20 推论3 三角形的一个外角大于任何一个和它不相邻的内角
2010年中考数学几何公式、定理汇编(二)
21 全等三角形的对应边、对应角相等
22边角边公理(SAS) 有两边和它们的夹角对应相等的两个三角形全等
23 角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等
24 推论(AAS) 有两角和其中一角的对边对应相等的两个三角形全等
25 边边边公理(SSS) 有三边对应相等的两个三角形全等
26 斜边、直角边公理(HL) 有斜边和一条直角边对应相等的两个直角三角形全等
27 定理1 在角的平分线上的点到这个角的两边的距离相等
28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上
29 角的平分线是到角的两边距离相等的所有点的集合
30 等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角)
31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边
32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合
33 推论3 等边三角形的各角都相等,并且每一个角都等于60°
34 等腰三角形的判定定理 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)
35 推论1 三个角都相等的三角形是等边三角形
36 推论 2 有一个角等于60°的等腰三角形是等边三角形
37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半
38 直角三角形斜边上的中线等于斜边上的一半
39 定理 线段垂直平分线上的点和这条线段两个端点的距离相等
40 逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上
2010年中考数学几何公式、定理汇编(三)
41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合
42 定理1 关于某条直线对称的两个图形是全等形
43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线
44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上
45逆定理 如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称
46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方,即a^2+b^2=c^2
47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ,那么这个三角形是直角三角形
48定理 四边形的内角和等于360°
49四边形的外角和等于360°
50多边形内角和定理 n边形的内角的和等于(n-2)×180°
51推论 任意多边的外角和等于360°
52平行四边形性质定理1 平行四边形的对角相等
53平行四边形性质定理2 平行四边形的对边相等
54推论 夹在两条平行线间的平行线段相等
55平行四边形性质定理3 平行四边形的对角线互相平分
56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形
57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形
58平行四边形判定定理3 对角线互相平分的四边形是平行四边形
59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形
60矩形性质定理1 矩形的四个角都是直角
2010年中考数学几何公式、定理汇编(四)
61矩形性质定理2 矩形的对角线相等
62矩形判定定理1 有三个角是直角的四边形是矩形
63矩形判定定理2 对角线相等的平行四边形是矩形
64菱形性质定理1 菱形的四条边都相等
65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角
66菱形面积=对角线乘积的一半,即S=(a×b)÷2
67菱形判定定理1 四边都相等的四边形是菱形
68菱形判定定理2 对角线互相垂直的平行四边形是菱形
69正方形性质定理1 正方形的四个角都是直角,四条边都相等
70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角
71定理1 关于中心对称的两个图形是全等的
72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分
73逆定理 如果两个图形的对应点连线都经过某一点,并且被这一
点平分,那么这两个图形关于这一点对称
74等腰梯形性质定理 等腰梯形在同一底上的两个角相等
75等腰梯形的两条对角线相等
76等腰梯形判定定理 在同一底上的两个角相等的梯形是等腰梯形
77对角线相等的梯形是等腰梯形
78平行线等分线段定理 如果一组平行线在一条直线上截得的线段
相等,那么在其他直线上截得的线段也相等
79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰
80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边
2010年中考数学几何公式、定理汇编(五)
81 三角形中位线定理 三角形的中位线平行于第三边,并且等于它的一半
82 梯形中位线定理 梯形的中位线平行于两底,并且等于两底和的一半 L=(a+b)÷2 S=L×h
83 (1)比例的基本性质 如果a:b=c:d,那么ad=bc;如果ad=bc,那么a:b=c:d
84 (2)合比性质 如果a/b=c/d,那么(a±b)/b=(c±d)/d
85 (3)等比性质 如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b
86 平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段成比例
87 推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例
88 定理 如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边
89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例
90 定理 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似
91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)
92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)
94 判定定理3 三边对应成比例,两三角形相似(SSS)
95 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似
96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比
97 性质定理2 相似三角形周长的比等于相似比
98 性质定理3 相似三角形面积的比等于相似比的平方
99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值
100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值
2010年中考数学几何公式、定理汇编(六)
101圆是定点的距离等于定长的点的集合
102圆的内部可以看作是圆心的距离小于半径的点的集合
103圆的外部可以看作是圆心的距离大于半径的点的集合
104同圆或等圆的半径相等
105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆
106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线
107到已知角的两边距离相等的点的轨迹,是这个角的平分线
108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线
109定理 不在同一直线上的三点确定一个圆。
110垂径定理 垂直于弦的直径平分这条弦并且平分弦所对的两条弧
111推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧
②弦的垂直平分线经过圆心,并且平分弦所对的两条弧
③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧
112推论2 圆的两条平行弦所夹的弧相等
113圆是以圆心为对称中心的中心对称图形
114定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等
115推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等
116定理 一条弧所对的圆周角等于它所对的圆心角的一半
117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等
118推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径
119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形
120定理 圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角
2010年中考数学几何公式、定理汇编(七)
121①直线L和⊙O相交 d<r
②直线L和⊙O相切 d=r
③直线L和⊙O相离 d>r
122切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线
123切线的性质定理 圆的切线垂直于经过切点的半径
124推论1 经过圆心且垂直于切线的直线必经过切点
125推论2 经过切点且垂直于切线的直线必经过圆心
126切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角
127圆的外切四边形的两组对边的和相等
128弦切角定理 弦切角等于它所夹的弧对的圆周角
129推论 如果两个弦切角所夹的弧相等,那么这两个弦切角也相等
130相交弦定理 圆内的两条相交弦,被交点分成的两条线段长的积相等
131推论 如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项
132切割线定理 从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项
133推论 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等
134如果两个圆相切,那么切点一定在连心线上
135①两圆外离 d>R+r ②两圆外切 d=R+r
③两圆相交 R-r<d<R+r(R>r)
④两圆内切 d=R-r(R>r) ⑤两圆内含d<R-r(R>r)
136定理 相交两圆的连心线垂直平分两圆的公共弦
137定理 把圆分成n(n≥3):
⑴依次连结各分点所得的多边形是这个圆的内接正n边形
⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形
138定理 任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆
139正n边形的每个内角都等于(n-2)×180°/n
140定理 正n边形的半径和边心距把正n边形分成2n个全等的直角三角形
141正n边形的面积Sn=pnrn/2 p表示正n边形的周长
142正三角形面积√3a/4 a表示边长
143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4
144弧长计算公式:L=n兀R/180
145扇形面积公式:S扇形=n兀R^2/360=LR/2
146内公切线长= d-(R-r) 外公切线长= d-(R+r)
2. 对应法则
(1) 解析法
就是用等式来表示一个变量是另一个变量的函数,这个等式叫做函数的解析表达式(函数关系式)
(2) 列表法
(3) 图像法
3 函数的值域
一般的,当函数f(x)的自变量x去定义域D中的一个确定的值a,函数有唯一确定的对应值这个对应值,称为x=a时的函数值,简称函数值,记作:f(a)
32 函数的图像
若把自变量x的一个值和函数y的对应值分别作为点的横坐标和纵坐标,可以在直角坐标平面上描出一个点(x,f(x))的集合构成一个图形F,而集F成为函数y=f(x)的图像
知道函数的解析式,要画函数的图像,一般分为列表,描点,连线三个步骤
4 正比例函数
41 正比例函数
一般地,函数y=kx(k是不等于零的常数)叫做正比例函数,其中常数k叫做变量y与x之间的比例函数确定了比例函数k,就可以确定一个正比例函数
正比例函数y=kx有下列性质:
(3) 当k>0时,它的图像经过第一,三象限,y随着x的值增大而增大;当k<0时,他的图像经过第二,四象限,y随着x的增大而减小
(2)随着比例函数的绝对值的增加,函数图像渐渐离开x轴而接近于y轴,因此,比例系数k和直线y=kx与x轴正方向所成的角有关据此,k叫做直线y=kx的斜率
42 反比例函数
一般地,函数y=k/x(k是不等于0的常数)叫做反比例函数
反比例函数y=k/x有下列性质:
(7) 当k>0时,他的图像的两个分支分别位于第一,三象限内,在每一个象限内,y随x的值增大而减小;当k<0时,它的图像的两个分支分别位于第二、四象限内,在每一个象限内,y随x的增大而增大
(8) 它的图像的两个分支都无限接近但永远不能达到x轴和y轴
5 一次函数及其图像
51 一次函数及其图像
如果k=0时,函数变形为y=b,无论x在其定义域内取何值,y都有唯一确定的值b与之对应,这样的函数我们称它为常函数
直线y=kx+b与y轴交与点(0,b),b叫做直线y=kx+b在y轴上的截距,简称纵截距
52 一次函数的性质
函数y=f(小),在a〈x〈b上,如果函数值随着自变量x的值增加而增加,那么我们说函数f(x)在a〈x
如果分别画出两个二元一次方程所对应的一次函数图像,交点的坐标就是这个方程组的解,这种求二元一次方程组的解法叫图像法
1. 函数的定义域
15.(几何证明选讲选做题)如图:PA与圆O相切于A,PCB为圆O的割线,并且不过圆心O,已知PA= ,PC=1,则|BC|=
.
,PC=1,则|BC|=
.

 清远市华侨中学2010届高三第一次统测2009.9.28
清远市华侨中学2010届高三第一次统测2009.9.28
14.(不等式选讲选做题)不等式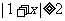 的解集是 .
的解集是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com