
P.38中习题五1、2、3.
补充:1.a、b为异面直线,a∥α,b∥α,a∥β,b∥β.
求证:α∥β.
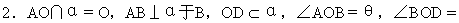
θ2,∠AOD=θ3.
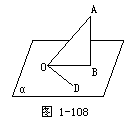
求证:cos·θ3=cosθ1·cosθ2.
(三)练习
例1 垂直于同一直线的两个平面平行.
已知:α⊥AA',β⊥AA',
求证:α∥β.
师提示:要证明两个平面平行,有两种方法:一是利用定义;二是利用判定定理,也是较常用的一种方法.因此利用判定定理证明例1的关键是:如何构造一个平面内的两相交直线都平行于另一个平面?
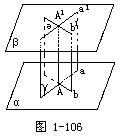
证明:设经过直线AA'的两个平面γ,δ分别与平面α、β交于直线a,a'和b,b'.
∵AA'⊥α,AA'⊥β,
∴AA⊥a,AA'⊥a',
∴a‖a',则a'∥α.
同理,b'∥α.
又∵a'∩b'= A'
∴α∥β.
师:这个例题的结论可与定理“垂直于同一平面的两条直线平行”联系起来记忆,也可作为判定两个平面平行的一种方法.
练习:判断下列命题的正误(幻灯显示).
1.垂直于同一直线的两直线平行.
2.分别在两个平行平面内的两条直线都平行(P.37中练习1).
3.如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行(P.38中练习2<1>).
4.如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行(P.38中练习2<2>).
答:1.错,这两条直线还可能相交或异面.
2.错,这两条直线还可能异面,但不会相交.
3.错,反例如图1-107.
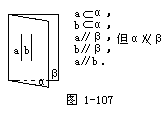
4.对.
(二)两个平面平行的判定
师:根据前一小节平面平行的定义,我们来判断两个互逆命题的正误,并说明理由(幻灯显示).
命题1.如果两个平面平行,那么其中一个平面内的所有直线一定都和另一个平面平行.
命题2.如果一个平面内的所有直线都和另一个平面平行,那么这两个平面平行.
生:命题1是正确的.因为在这些直线中如果有一条和另一个平面有公共点,这点也必是这两个平面的公共点.那么这两个平面就不可能平行了.
命题2也是正确的.因为如果这两个平面有公共点,那么在另一个平面内通过这点的直线就不可能平行于另一个平面.
师:通过上面的讨论我们知道:两个平面平行的问题可转化为一个平面内直线和另一个平面平行的问题.实际上判定两个平面平行的条件不需要一个平面内的所有直线都平行于另一个平面,只需要在一个平面内有两条相交直线都平行于另一个平面.
两个平面平行的判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.
师:我们知道,一个定理只有经过证明才能说明它的正确性并直接应用,下面我们来证明这个定理.
已知:在平面β内,有两条相交直线a、b和平面α平行.
求证:β∥α.
师分析:要证明这个定理,先思考几个问题(提出问题并启发学生得出结论)(幻灯显示).
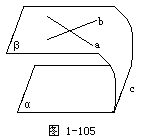
问题1:如果平面α与平面β不平行,那么它们的位置关系怎样?(相交).
问题2:若平面α与平面β相交,那么交线与平行于平面α的直线a和b各有什么关系?(平行).
问题3:相交直线a和b都与交线平行合理吗?(不合理,与平行公理矛盾).
师:总结得出证明定理应该根据定义,利用反证法,让学生写出它的证明过程.
证明:假设α∩β=c.
a∥α,a∩β,
a∥c,同理b∥c.
a∥b,这与题设a与b相交矛盾
α∥β.
师:在实际生活中,也经常利用这个判定定理判断两个平面平行.如在判断一个平面是否水平时,把水准器放在这个平面上交叉放两次,如果水准器的气泡都是居中的,就可以判定这个平面和水平面平行.
下面请同学们完成例1和练习.
1.12两个平面的位置关系及1.13两个平面平行的判定和性质这两个课题调整安排为2课时.本节课为第一课时,主要讲解两个平面的位置关系及两个平面平行的判定.
3.教学疑点:正确理解并应用两个平面平行的判定定理时,要注意定理中的关键词:相交.
2.教学难点:掌握两个平面平行的判定定理的证明及其应用.
1.教学重点:掌握两个平面的位置关系;掌握两个平面平行的判定.
(三)德育渗透点
让学生认识研究两个平面的位置关系以及掌握和应用两个平面平行的判定是实际生产的需要,体现了理论联系实践的原则,并更好地培养学生分析问题与解决问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com