
19.解:(Ⅰ)设恰有3名同学所抽靶位号与其号码相同的事件为A,则事件A所包含的基本事件的种数为2C,而六名同学通过抽签排到1~6号靶位的排法种数为A. ……3分
由于每位同学通过抽签排到某个靶位是等可能的,所以P(A)==.
答:恰有3名同学所抽靶位号与其号码相同的概率为. ……………………………6分
(Ⅱ)设该同学恰好击中28环、29环、30环的事件分别为B,C,D, 他能获得射击标兵称号的事件为E,则事件B,C,D彼此互斥。
∵P(B)=C×(0.1)2×0.2+ C×0.1×(0.2)2=0.018,
P(C)=C×(0.1)2×0.2=0.006,
P(D)= (0.1)3=0.001,…………………………………………………………………10分
∴P(E)=P(B+C+D)=P(B)+P(C)+P(D)=0.018+0.006+0.001=0.025.
答:该同学能获得射击标兵称号的概率为0.025.……………………………………13分
[链接高考]概率是新课程中理科加重的一部分内容之一,从前几年的高考来看都有不同难度的对学生进行考查。
18.解:(Ⅰ)建立如图所示的空间坐标系,则A(0,0,2),B(2,0,0),C(2,4,0),
D(0,2,2),G(2,2,0),F(0,3,0).
(1)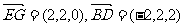 ,…………………………………………2分
,…………………………………………2分
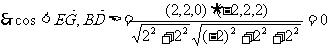 ,
,
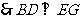 .…………………………………………………………………5分
.…………………………………………………………………5分
(Ⅱ)
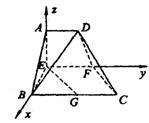 设面ABCD的法向量为
设面ABCD的法向量为 ,
,
即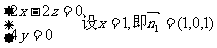 ,……………………7分
,……………………7分
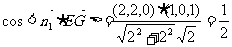 ,
,
EG和平面ABCD所成的角为30°.…………………………………………10分
(Ⅲ)设平面DFC的法向量为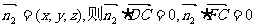 ,
,
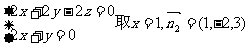 ,……………………12分
,……………………12分
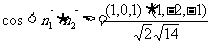 ,
,
∴所以二面角B-DC-F的斜弦值为0.…………………………………………14分
此题还可用几何证明的方法.
[链接高考]立几中对空间的线线、线面、面面关系的考查是主线, 在理科生中对空间向量的要求也是课标要求.
17.解:(Ⅰ) 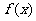 的定义域为
的定义域为 , …..1分
, …..1分
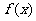 的导数
的导数 . …………..3分
. …………..3分
令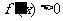 ,解得
,解得 ;令
;令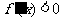 ,解得
,解得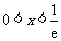 .
.
从而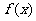 在
在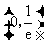 单调递减,在
单调递减,在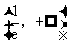 单调递增.
……..5分
单调递增.
……..5分
所以,当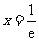 时,
时,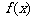 取得最小值
取得最小值 . ……..6分
. ……..6分
(Ⅱ)依题意,得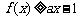 在
在 上恒成立,
上恒成立,
即不等式 对于
对于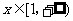 恒成立 .
…………..8分
恒成立 .
…………..8分
令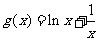 , 则
, 则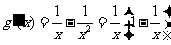 .
…………..10分
.
…………..10分
当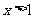 时,因为
时,因为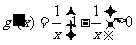 ,
,
故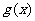 是
是 上的增函数, 所以
上的增函数, 所以  的最小值是
的最小值是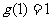 ,
,
从而 的取值范围是
的取值范围是 .
…………..13分
.
…………..13分
[链接高考]这是一个导数的基本运用考查,考查学生的基本概念的清楚掌握、基本运算的熟练程度,属于容易题,问题的关键在于细心和规范。
16.解:(Ⅰ)由 得
得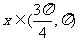 ,…..2分
,…..2分
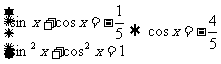 .
…..6分
.
…..6分
(Ⅱ)由(Ⅰ)得sinx=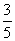
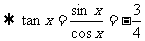 ,
…..7分
,
…..7分
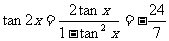 ,
…..9分
,
…..9分
 .
…..12分
.
…..12分
[链接高考]本小题是与整份试卷中三角部分相配套,侧重考查学生对三角中的基本函数-sinx,cosx,tanx的掌握程度,这也是新课程的要求.
(二)选做题(13-15题,考生只能从中选做两题)
13.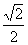 [解析]点(1,0)的直角坐标为(1,0),直线的直角坐标方程为x+y-2=0,
[解析]点(1,0)的直角坐标为(1,0),直线的直角坐标方程为x+y-2=0,
所以点到直线的距离为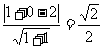 .
.
[链接高考]极坐标的问题主要是把它转化为直角坐标中来解决,当然也可以在极坐标系中解决.
14. 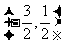 [解析]可以用分类讨论去绝对值的方法,也可以用数轴的方法解.
[解析]可以用分类讨论去绝对值的方法,也可以用数轴的方法解.
[链接高考]不等式选讲主要考查均值不等式、含有绝对值的不等到式和柯西不等式.
15.[解析]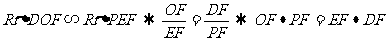 ;
;
又相交弦定理得:DF FE=BF
FE=BF AF,所以
AF,所以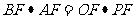 ;
;
设OF=x,BF=2-x,AF=2+x,PF=4-x代入可求得x=1,即PF=3.
[链接高考]本小题主要考查圆中相交弦、圆周角等几何知识,同时也考查了方程的思想.
(一)必做题(9-12题)
9.甲、甲[解析]甲平均成绩为70;乙平均成绩为68;甲方差为2,乙方差为7。2;所以平均成绩较高的和成绩较稳定都是甲.
[链接高考]统计是新教材新高考新增的考点,07年高考有一大题,属于应用方面,要加强.
10.2[解析]连接AC则有AC=5,据定义有CA-CB=2=2a,2c=4,所以e=2.
[链接高考]本小题考查圆锥曲线的定义、图象和性质,属于基本题型.
11.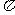 [解析]由题设信息知:
[解析]由题设信息知: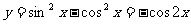 ,所以周期
,所以周期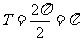 .
.
[链接高考]本小题是一个信息分析题,近几年高考经常出现,要平时注意加强.
12.①③[解析]①复数为 -1+2i所对应的点在第二象限; ②x=1,y=4时满足条件;③原命题和逆否命题、逆命题与否命题是等价命题;④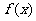 的定义域为实数集的充要条件是
的定义域为实数集的充要条件是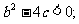 值域为实数集的充要条件是
值域为实数集的充要条件是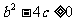 .
.
8.A[解析]充分运用向量的几何形式运算及向量平行的定理及推论,把相关向量用已知向量表示即可.
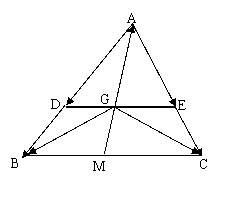
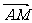
 因为
因为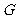 是
是 的重心,
的重心,
所以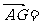
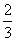
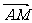 =
=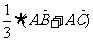 ;由
;由 D、
D、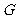 、E三点共线,有
、E三点共线,有 共线,
共线,
所以,有且只有一个实数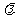 ,
, 
而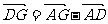

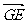 =
=
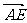 -
-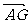 =
=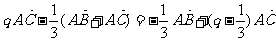 ,
,
所以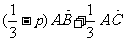 =
=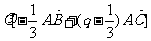 .又因为
.又因为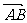 、
、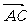 不共线,所以
不共线,所以
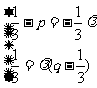 ,消去
,消去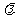 ,整理得3
,整理得3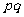 =
=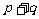 ,故
,故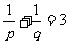 .
.
另解:可取特殊点,DGE平行BC.
[链接高考]建立p与q的关系关键是由D,G,E三点共线得出.为此要熟练运用已知向量表示未知向量,
平面向量是高中数学中最基本、最常用、最常考的知识之一,注意平面向量与其他知识的联系.
7.D[解析]分别作出区域M、N,则公共部分的面积为
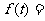
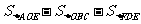
=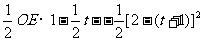
=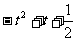 ,选(D).
,选(D).
[链接高考]线性规划是新教材新增内容,它具有数形结的功能,很容易与解几、函数等知识综合考查.
6.C[解析]①中的反例是“墙角”,②③是正确的.
 [链接高考]本小题考查立几中线面、面面的关系,是新课程的要求,做此类问题要讲究方法,充分利用笔和纸做模型来帮助。
[链接高考]本小题考查立几中线面、面面的关系,是新课程的要求,做此类问题要讲究方法,充分利用笔和纸做模型来帮助。
5.D[解析]由流程图可得出此函数既是奇函数又存在零点,因此选D.
[链接高考]本小题主要考查框图知识和数列知识,以及分析问题和解决问题的能力. 算法初步是高考新增的考点.近两年每年都有一道小题,常与函数、数列等知识进行小综合来考查,估计以后的考查形式不会有大的变化.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com