
考纲点击:掌握函数的奇偶性的定义及图象特征,并能判断和证明函数的奇偶性,能利用函数的奇偶性解决问题.
热点提示:1.函数的奇偶性作为函数的一个重要性质,常与函数的单调性、周期性等知识交汇命题
2.每年的高考试题中,各种题型都可能出现,多以小题形式出现,属中低档题
本节复习重点:函数的奇偶性的定义及应用.
8.如图13,已知:C是以AB为直径的半圆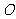 上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连结AE并延长交BD于点F,直线CF交AB的延长线于点G.
上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连结AE并延长交BD于点F,直线CF交AB的延长线于点G.
(1)求证:点F是BD中点;
(2)求证:CG是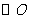 的切线;
的切线;
(3)若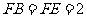 ,求
,求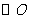 的半径.
的半径.
7.如图12,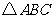 是
是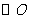 的内接三角形,
的内接三角形,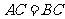 ,
,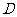 为
为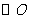 中上一点,延长
中上一点,延长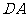 至点
至点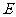 ,使
,使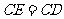 .
.
(1)求证: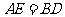 ;
;
(2)若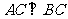 ,求证:
,求证: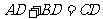 .
.

6.如图11,已知AC切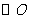 于A,
于A,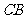 顺次交
顺次交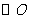 于
于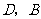 两点,
两点,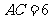 ,
,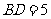 ,连结AD,AB.
,连结AD,AB.
(1)求证: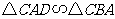 ;
;
(2)求线段DC的长.
5.如图10,D是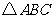 边AB上一点,DE交AC于点E,
边AB上一点,DE交AC于点E,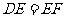 ,
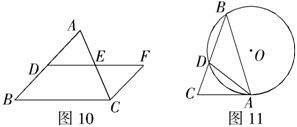
,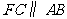 .求证:
.求证: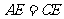 .
.
4.如图9,在Rt△ABC中,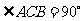 ,
,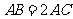 ,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且
,DE垂直平分BC,垂足为D,交AB于点E.又点F在DE的延长线上,且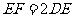 .求证:四边形ACEF是菱形.
.求证:四边形ACEF是菱形.
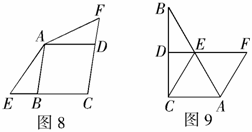
3.如图8,菱形ABCD中,E、F分别为CB、CD延长线上的点,且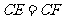 .求证:
.求证: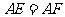 .
.
1.下列命题中真命题的个数是( )
①两个相似多边形面积之比等于相似比的平方;
②两个相似三角形的对应高之比等于它们的相似比;
③在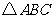 与
与 中,
中,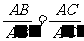 ,
,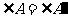 ,那么
,那么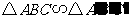 ;
;
④已知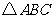 及位似中心
及位似中心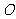 ,能够作一个且只能作一个三角形,使位似比为0.5.
,能够作一个且只能作一个三角形,使位似比为0.5.
(A)1个 (B)2个 (C)3个 (D)4个
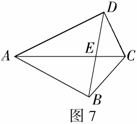 2.已知如图7,在四边形ABCD中,对角线AC,BD交于点E,且AC平分∠DAB,AB=AE,AC=AD.下四个结论:①AC⊥BD;②CB=DE;③
2.已知如图7,在四边形ABCD中,对角线AC,BD交于点E,且AC平分∠DAB,AB=AE,AC=AD.下四个结论:①AC⊥BD;②CB=DE;③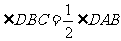 ;④△ABE是等边三角形.请写出正确的结论序号____________(把你认为正确的结论序号填上,并证明其中一个).
;④△ABE是等边三角形.请写出正确的结论序号____________(把你认为正确的结论序号填上,并证明其中一个).
21.解:(Ⅰ)在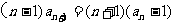 中,
中,
由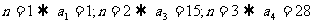 ;
;
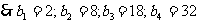 . …..3分
. …..3分
(Ⅱ)由(1)知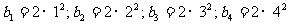 .由此猜测
.由此猜测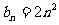 …..4分
…..4分
下面用数学归纳法证明:
①当n=1时猜想显然成立;
②假设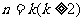 猜想成立,即
猜想成立,即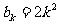 ,则有
,则有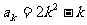 ,
,
根据题意,得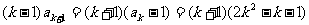 ,解出
,解出 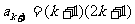 ,
,
于是 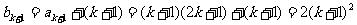 ,即当n=k+1时猜想也成立.
,即当n=k+1时猜想也成立.
综合①②得对于所有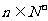 都有
都有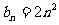 . …..8分
. …..8分
(Ⅲ)由(Ⅱ)知,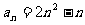 . …..9分
. …..9分
假设存在非零常数p,q,使得数列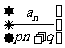 成等差数列,设其公差为d,
成等差数列,设其公差为d,
令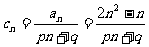 ,则有
,则有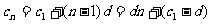 ,
,
从而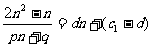 ,
,
化简得: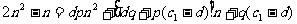 …..11分
…..11分
所以有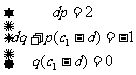 ,
,
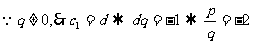 .
…..13分
.
…..13分
故存在满足关系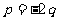 的非零常数p,q,使得数列
的非零常数p,q,使得数列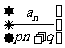 成等差数列.…..14分
成等差数列.…..14分
[链接高考]数列往往是难度较高的题,主要考查学生的探究能力,从近几年的高考来观察可发现数列对选拔性取着非常重要的作用.
20.解:(Ⅰ)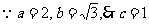 .
…..1分
.
…..1分
椭圆的焦点在y轴上,即F(0,1),F关于直线x-y=0对称的点为(1,0); …..2分
而抛物线的焦点坐标为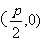 即得p=2,所以所求抛物线的方程为
即得p=2,所以所求抛物线的方程为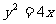 . …..5分
. …..5分
(Ⅱ)证明:设M,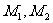 的坐标分别为
的坐标分别为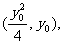
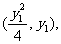
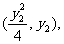
由A、M、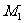 三点共线得:
三点共线得: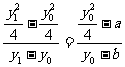 , …..7分
, …..7分
化简得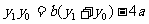 ,
,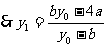 ;
;
同理,由B、M、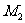 三点共线得:
三点共线得: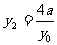 . …..9分
. …..9分
设(x,y)是直线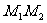 上的任意一点,则
上的任意一点,则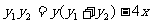 ; …..10分
; …..10分
把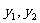 代入上式整理得:
代入上式整理得: ;
;
由M是任意的,则有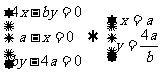 , …..13分
, …..13分
所以动直线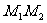 恒过定点
恒过定点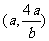 . …..14分
. …..14分
[链接高考]圆锥曲线和直线是解析几何的主线,考查学生的运算能力是解析几何的重要部分,特别是包含比较多字母的运算,同时也考查了“设而不求”的解题策略和数形结合的数学思想方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com