
2.∵二次函数
在 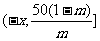 上递增,在
上递增,在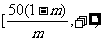 上递减
上递减
∴适当地涨价,即 x > 0 , 即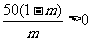
就是 0 < m <1 , 能使销售总金额增加。
2.如果适当的涨价,能使销售总金额增加,求m的取值范围。
解:1.设商品现在定价a元,卖出的数量为b个。
由题设:当价格上涨x%时,销售总额为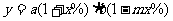
即 
取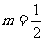 得:
得:
当 x = 50时,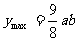
即该商品的价格上涨50%时,销售总金额最大。
已知某商品的价格每上涨x%,销售的数量就减少mx%,其中m为
正常数。
1.当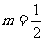 时,该商品的价格上涨多少,就能使销售的总金额最大?
时,该商品的价格上涨多少,就能使销售的总金额最大?
某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件,为估计以后每月的产量,以这三个月的产量为依据,用一个函数模拟该产品的月产量y与月份x的关系,模拟函数可选用二次函数或 (a,b,c为常数),已知四月份该产品的产量为1.37万件,请问:用以上那个函数作模拟函数较好?说明理由。
(a,b,c为常数),已知四月份该产品的产量为1.37万件,请问:用以上那个函数作模拟函数较好?说明理由。
解:设二次函数为: 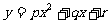
由已知得:
∴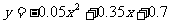
当 x = 4时,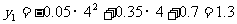
又对于函数 
由已知得: ∴
∴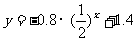
当 x = 4时,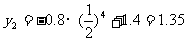
由四月份的实际产量为1.37万件,
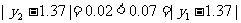
∴选用函数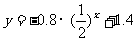 作模拟函数较好。
作模拟函数较好。
8.设{an}的公比为q,{bn}的公差为d,据题意,得
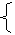 |
a1+0=1, |
① |
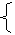 |
a1q2+2d=2a, |
③ |
|
a1q+d=a, |
② |
a1q3+3d=2. |
④ |
由①、②、③、④,解得a1=1,q=2,d=-2, ∴ an=2n-1,bn=-2(n-1),cn=2n-1-2(n-1). ∴ Tn=(1-0)+(2-2)+(22-4)+…+[2n-1-2(n-1)] =(1+2+22+…+2n-1)-[2+4+…+2(n-1)]=2n-1-n(n-1). 9.(1)n≥1时,S2n+1=an+1(Sn+1+k). ∵ an+1=Sn+1-Sn,消去an+1,得 S2n+1=(Sn+1-Sn)(Sn+1+k), ∴ SnSn+1=(Sn+1-Sn)k, ∴ (1/Sn)-(1/Sn+1)=(1/k). (2)由(1)得(1/Sn+1?)-(1/Sn)=-(1/k),∴ {(1/Sn)}是以-(2/k)为首项,-(1/k)为公差的等差数列, ∴ (1/Sn)=-(2/k)+(n-1)(-(1/k))=-(n+1/k), ∴ Sn=-(k/n+1). (3)设cn=(n/(pn+q)Sn)=-(n2+n)/[k(pn+q)]. ∵ cn成等差数列,∴ cn=c1+(n-1)d, ∴ -n2-n=k(pn+q)(nd+c1-d)=kdpn2+[kdq+kp(c1-d)]n+kq(c1-d),
∴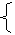 |
kdp=-1, |
得p=q, |
|
kdq+kp(c1-d)=-1, |
||
|
kq(c1-d)=0 |
∴ (p/q)=1. ∴ (p/q)是与k无关的常数1. 10.(1)∵a?3-a1=2d,f(x)=(x-1)2, ∴f(d+1)-f(d-1)=2d, 即d2-(d-2)2=2d. 解得d=2.从而a1=f(1)=0, ∴an=2n-2.? 由(b3/b1)=q2,得(q-2)2/q2=q2.解得 q=-2.从而b1=f(-1)=4, ∴bn=4·(-2)n+1. (2)令xn=(cn/bn),则x1=a2=2,当n≥2时,xn=an+1-an=2,∴xn=2(n∈N),从而cn=2bn.∴Sn=2(b1+b2+…+bn) =(8/3)[1-(-2)n].
故?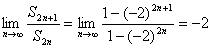 . . |
?§?2 数列的综合应用
1.B;2.C;3.A;4.D;5.-1或1;6.1;
7.24.
8.(1)当n=1时,a1=S1=(π/4);?
当n≥2时,
an=Sn-Sn-1=…=(π/12)(4n-1).
∴ an=(π/12)(4n-1)(n∈N).
从而an+1-an=…=(π/3),?
∴ {an}是首项为(π/4),公差为(π/3)的等差数列.
(2)因为an=(π/12)(4n-1),且4n-1是奇数,所以an≠kπ(k∈Z),从而sinan≠0,即bn≠0(n∈N).
∵ (bn+1/bn)=(sinan+3)/sinan=sin(an+3×(π/3))/(sinan)=-1,
又b1=sina1·sina2·sina3=sin(π/4)sin(7π/12)·sin(11π/12)
=(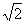 /2)·(1/2)(cos(π/3)-cos(3π/2))=(
/2)·(1/2)(cos(π/3)-cos(3π/2))=(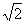 /8),?
∴ {an}是首项为(
/8),?
∴ {an}是首项为(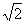 /8),公比为-1的等比数列,从而对任何n∈N,都有bn=(
/8),公比为-1的等比数列,从而对任何n∈N,都有bn=(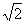 /8)(-1)n-1.
9.(1)由韦达定理,得p+q=
/8)(-1)n-1.
9.(1)由韦达定理,得p+q=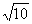 ,pq=t2,又由p,p-q,q成等比数列,有(p-q)2=pq,∴(p+q)2=5pq=5t2,t2=2.∵t>0,?∴t=
,pq=t2,又由p,p-q,q成等比数列,有(p-q)2=pq,∴(p+q)2=5pq=5t2,t2=2.∵t>0,?∴t=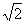 (2)用拆项相消法,得Sn=1-1/(n+1),故只要证明log2
(2)用拆项相消法,得Sn=1-1/(n+1),故只要证明log2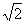 ≤1-(1/n+1)<log
≤1-(1/n+1)<log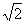 2,即要证(1/2)≤1-1/(n+1)<2,右侧不等式显然成立,左侧不等式即为1/(n+1)≤(1/2),显然成立.
10?(1)设小李这笔贷款额应为y元,由题意,得 (y+13334)×40%=13334,
∴ y=(13334/40%)-13334≈2.00×104(元).
答:小李应向银行贷款2.00×104(元).
(2)设小李每年应还x元,由已知10年还清.
一年后贷款余额为20000(1+10%)-x,
二年后贷款余额为[20000(1+10%)-x](1+10%)-x
=20000(1+10%)2-x(1+10%)-x
……
10年后的贷款余额为
20000(1+10%)10-x(1+10%)9-…-x(1+10%)-x,
据题意,得
20000(1+10%)10-x[1+(1+10%)+(1+10%)2+…+(1+10%)9]=0.
解得 x=(20000×0.1×1.110/1.110-1),
∵ 1.110=(1+0.1)10=1+10×0.1+C210×0.01+C310×0.001+C410×0.0001+…=1+1+0.45+0.021+0.00252+…≈2.5937,
∴ x≈3255(元).
答:小李每年应还3255元.
?§?3 数学归纳法
1.略;
2.Ⅱ1=(3/4),Ⅱ2=(2/3),Ⅱ3=(5/8),为统一形式,将Ⅱ2表示为(4/6),由此推测:Ⅱn=(n+2/2n+2).再用数学归纳法证明.
3.略.
4.∵ (n2-1)/(n2+1)=1-2/(n2+1),
f(
2,即要证(1/2)≤1-1/(n+1)<2,右侧不等式显然成立,左侧不等式即为1/(n+1)≤(1/2),显然成立.
10?(1)设小李这笔贷款额应为y元,由题意,得 (y+13334)×40%=13334,
∴ y=(13334/40%)-13334≈2.00×104(元).
答:小李应向银行贷款2.00×104(元).
(2)设小李每年应还x元,由已知10年还清.
一年后贷款余额为20000(1+10%)-x,
二年后贷款余额为[20000(1+10%)-x](1+10%)-x
=20000(1+10%)2-x(1+10%)-x
……
10年后的贷款余额为
20000(1+10%)10-x(1+10%)9-…-x(1+10%)-x,
据题意,得
20000(1+10%)10-x[1+(1+10%)+(1+10%)2+…+(1+10%)9]=0.
解得 x=(20000×0.1×1.110/1.110-1),
∵ 1.110=(1+0.1)10=1+10×0.1+C210×0.01+C310×0.001+C410×0.0001+…=1+1+0.45+0.021+0.00252+…≈2.5937,
∴ x≈3255(元).
答:小李每年应还3255元.
?§?3 数学归纳法
1.略;
2.Ⅱ1=(3/4),Ⅱ2=(2/3),Ⅱ3=(5/8),为统一形式,将Ⅱ2表示为(4/6),由此推测:Ⅱn=(n+2/2n+2).再用数学归纳法证明.
3.略.
4.∵ (n2-1)/(n2+1)=1-2/(n2+1),
f(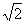 )=(2(n/2)-2-(n/2))/(2(n/2+2-(n/2))=(2n-1)/(2n+1)=1-2/(2n+1),
∴ 只需比较2n与n2的大小.
可用“归纳-猜想-证明”的方法来解决,也可以利用二项式定理.
下略.
当n=1或n≥5时,f(
)=(2(n/2)-2-(n/2))/(2(n/2+2-(n/2))=(2n-1)/(2n+1)=1-2/(2n+1),
∴ 只需比较2n与n2的大小.
可用“归纳-猜想-证明”的方法来解决,也可以利用二项式定理.
下略.
当n=1或n≥5时,f(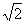 )>(n2-1)/(n2+1);?当n=2,4时,f(
)>(n2-1)/(n2+1);?当n=2,4时,f(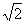 )=(n2-1)/(n2+1);当n=3时,f(
)=(n2-1)/(n2+1);当n=3时,f(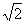 )<(n2-1)/(n2+1).
5.(1)当n=1时,有a1+S1=3,即a1=(3/2);?
当n≥2时,Sn+an=2n+1, ①
则 ?Sn+1+an+1=2n+3. ②
②-①,得(Sn+1-Sn)+an+1-an=2,
∴ an+1=(1/2)an+1.
由此得a2=(7/4),a3=(15/8).
(2)猜想:an=(2·2n-1)/2n=2-(1/2n) (n∈N),证明略.
6.(1)设{an}的公差为d,则
)<(n2-1)/(n2+1).
5.(1)当n=1时,有a1+S1=3,即a1=(3/2);?
当n≥2时,Sn+an=2n+1, ①
则 ?Sn+1+an+1=2n+3. ②
②-①,得(Sn+1-Sn)+an+1-an=2,
∴ an+1=(1/2)an+1.
由此得a2=(7/4),a3=(15/8).
(2)猜想:an=(2·2n-1)/2n=2-(1/2n) (n∈N),证明略.
6.(1)设{an}的公差为d,则
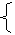 |
a1+d=8, |
解得a1=5,d=3. |
|
10a1+(10×9)/2d=185, |
∴ an=a1+(n-1)d=3n+2. (2)Sn=a2+a4+a8+…+a2n=(3×2+2)+(3×4+2)+…+(3×2n+2) =3×(2-2n+1)/(1-2)+2n=3×2n+1+2n-6. ∴ (Sn-2n)/3n=(3×2n+1-6)/3n=6×(2/3)n-6×(1/3)n,
∴ ?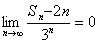 . . |
(3)∵ Tn=n(an+9)=3n2+11n,
∴ Sn-Tn=3(2n+1-n2-3n-2).
欲证n≥4时,Sn>Tn,只需证当n≥4时,2n+1>n2+3n+2.
证法1.数学归纳法(此处略).
证法2.利用二项式定理.
当n≥4时,2n+1=(1+1)n+1?
=C0n+1+C1n+1+C2n+1+…+Cn-1n+1+Cn+1n+1
≥2(C0n+1+C1n+1+C2n+1)=n2+3n+4>n2+3n+2,
即当n≥4时,2n+1>n2+3n+2,
∴ 当n≥4时,Sn>Tn.
7.∵ f(1)=36,f(2)=108=3×36,
?f(3)?
=360=10×36,…
∴ 猜想:f(n)能被36整除.
可用数学归纳法证明,略.
因为当m取大于36的整数时,f(1)=36不能被m整除,所以m=36为最大.
8.存在bn=3n+1,取n=1,2,3,从特殊归纳出一般结论,再用数学归纳法证明(略).
专题能力测试
一、?1.B;2.C;3.B;4.D;5.C;6.B;7.C;8.D;9.B;10.B;11.D;12.C.?
二、13.(1/n);14.219.01;
15.m>8;16.an=n+1.
三、17.首先应确定三数的大小关系,而且由“公差为1”知这三数是单调递增的.记x=10a2+81a+207,y=a+2,z=26-2a.由对数的定义域知x>0,y>0,z>0,故有-2<a<13.?
作差比较知x最大,而y-z=3(a-8),因a=8时y=z,不符题意,故分-2<a<8和8<a<13两种情况讨论:
(1)-2<a<8时,y<z,这时由lgz-lgy=lgx-lgz=1,得x=10z,z=10y,即10a2+81a+207=10(26-2a),26-2a=10(a+2),解得a=(1/2).
(2)当8<a<13时,z<y,这时由lgy-lgz=lgx-lgy=1,得x=10y,y=10z,即10a2+81a+207=10(a+2),a+2=10(26-2a),这时无解.
综合(1)(2)知a=(1/2).
18.设能构造这样的等比数列,并且其公比为q.则由条件知a1+a6=11,a1a6=(32/9),即a1=(1/3),a6=(32/3)或a1=(32/3),a6=(1/3).
对a1=(1/3),a6=(32/3),q=2,an=(1/3)2n-1,由(2/3)am-1+am+1+(4/9)=2am2,解得m=2,能使条件成立.
对a1=(32/3),a6=(1/3),同上法,可知其无解.
故能构造出题设的等比数列,其通项公式为an=(1/3)2n-1.
19.(1)当q=1时,Sn=na,Gn=na2.
∵ a≠0,∴ 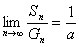 .
当0<q<1时,
.
当0<q<1时,
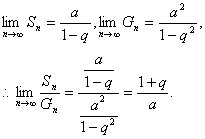
(2)∵ S1=a1=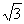 ,而Sn2=3+(n-1)=n+2,
∴ Sn=
,而Sn2=3+(n-1)=n+2,
∴ Sn=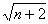 (n∈N).
当n≥2时,
an=Sn-Sn-1=
(n∈N).
当n≥2时,
an=Sn-Sn-1=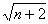 -
-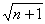 .
当n=1时,S1=
.
当n=1时,S1=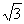 ,3a1=3
,3a1=3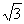 ,∴ S1<3a1. 又当n≥2时,33
Sn-3nan=
,∴ S1<3a1. 又当n≥2时,33
Sn-3nan=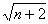 -3n(
-3n(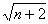 -
-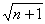 )?
=3n
)?
=3n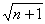 -(3n-1)·
-(3n-1)·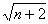 .?
∵ [3n
.?
∵ [3n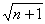 ]2-[(3n-1)
]2-[(3n-1)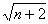 ]2
=…=-3n2+11n-2
=-3(n-(11/6))2+(97/12).
∴ 当n=2,3时,Sn>3nan;
当n≥4时,?Sn<3nan.?
20.(1)设第n年甲、乙产品年创外汇分别为an、bn(万元),则
an=32×2.25n-1?(万元),
bn=216×(2/3)n-1(万元).
令an>bn,
则32×2.25n-1>216×(2/3)n-1,
即32×(9/4)n-1>216×(2/3)n-1,
32×(3/2)2n-2>216×(2/3)n-1,
(3/2)3n-5>3.
3n>5+lg3/(lg3-lg2),n>2.57,∴ 取n=3.
答:从第三年开始,甲产品年创外汇超过乙产品年创外汇.
(2)设该企业第n年所创外汇为yn,则
yn=an+bn=32×(3/2)2n-2+216×(2/3)n-1?
=32×(3/2)2n-2+108×(2/3)n-1+108×(2/3)n-1
≥3
]2
=…=-3n2+11n-2
=-3(n-(11/6))2+(97/12).
∴ 当n=2,3时,Sn>3nan;
当n≥4时,?Sn<3nan.?
20.(1)设第n年甲、乙产品年创外汇分别为an、bn(万元),则
an=32×2.25n-1?(万元),
bn=216×(2/3)n-1(万元).
令an>bn,
则32×2.25n-1>216×(2/3)n-1,
即32×(9/4)n-1>216×(2/3)n-1,
32×(3/2)2n-2>216×(2/3)n-1,
(3/2)3n-5>3.
3n>5+lg3/(lg3-lg2),n>2.57,∴ 取n=3.
答:从第三年开始,甲产品年创外汇超过乙产品年创外汇.
(2)设该企业第n年所创外汇为yn,则
yn=an+bn=32×(3/2)2n-2+216×(2/3)n-1?
=32×(3/2)2n-2+108×(2/3)n-1+108×(2/3)n-1
≥3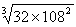 =216.
当且仅当108×(2/3)n-1=32×(3/2)2n-2,即n=2时,yn取得最小值216.
所以第二年,即2001年该企业创外汇最少为216万元,该年甲产品创外汇72万元,乙产品创外汇144万元.
(3)∵ y4=a4+b4=428.5>140×3=420,
∴ 该企业到2003年能进入国家重点企业.
=216.
当且仅当108×(2/3)n-1=32×(3/2)2n-2,即n=2时,yn取得最小值216.
所以第二年,即2001年该企业创外汇最少为216万元,该年甲产品创外汇72万元,乙产品创外汇144万元.
(3)∵ y4=a4+b4=428.5>140×3=420,
∴ 该企业到2003年能进入国家重点企业.
25、(1)b c (2)c (3)80%
24、①一个化学反应其正、逆反应过程的能量变化,在数值上相等,吸收与放出相反。(能量守恒)②一个化学反应的能量变化量与其反应物的物质的量有关(或成正比)③一个化学反应的能量变化量与其反应物、生成物的状态(固、液、气)有关。
23、(1)K>Na>Mg (2)NaOH (3)H2O,2K+2H2O=2KOH+H2↑,>(4)NaBr,黄色(5)略(6)Al(OH)3,Al(OH)3+ OH-= AlO2-+2H2O(中等题)
25. (8分)将1
mol SO2和含2mol氧气的空气放入一定体积的密闭容器中,550℃时,在催化剂作用下发生反应:2SO2+O2 2SO3反应达到平衡后,
O2的物质的量为1.6mol。
(8分)将1
mol SO2和含2mol氧气的空气放入一定体积的密闭容器中,550℃时,在催化剂作用下发生反应:2SO2+O2 2SO3反应达到平衡后,
O2的物质的量为1.6mol。
请回答下列问题:
(1)判断该反应达到平衡状态的标志是_______。(填字母)
a.SO2和SO3浓度相等 b.SO2百分含量保持不变
c.容器中气体的压强不变 d.SO3的生成速率与SO2的消耗速率相等
e.容器中混合气体的密度保持不变
(2)欲提高SO2的转化率,下列措施可行的是_______。(填字母)
a.向装置中再充入N2 b.向装置中再充入O2
(3)求该反应达到平衡时SO2的转化率(用百分数表示)。
|
考场 |
|
|
考号 |
|
24.(6分)研究表明,在一定温度和压强下,2 molH2(g)和1 molO2(g)完全化合生成2 molH2O(g)所放出的热量:①与在相同条件下2 molH2O(g)完全分解为2 molH2(g)和1 molO2(g)所吸收的热量在数值上相等;②是相同条件下1molH2(g)和0.5 molO2(g)完全化合生成1 molH2O(g)所放出热量的2倍;③比在相同条件下2 molH2(g)和1 molO2(g)完全化合生成2 molH2O(l)所放出的热量少。由此,你得出哪些结论?
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com