2.( 09天津理)已知函数若则实数的取值范围是　　　　　

1.(09福建理)函数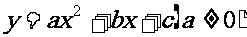的图象关于直线对称。据此可推测，对任意的非零实数a，b，c，m，n，p，关于x的方程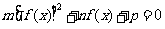的解集都不可能是(　　 )

A. 　　　　　B 　　　　　C 　　　D

2．讨论二次函数的区间根的分布情况一般需从三方面考虑：①判别式； ②区间端点的函数值的符号；　 ③对称轴与区间的相对位置．

二次函数是高考考查的永恒主题

5.主要方法：

讨论二次函数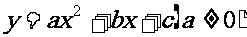在指定区间[m,n]上的最值问题：①注意对称轴与区间 [m,n]的相对位置；

②函数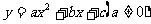在区间[m,n]上的单调性.

4.一元二次方程的根的分布问题：

(1)方程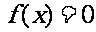有两个正根：

(2)方程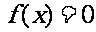有两个负根：

(3)方程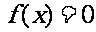有一个正根一个负根：

(4)方程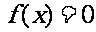有两个实根都小于k：

(5) 方程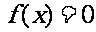有两个实根都大于k：

(6)方程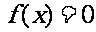有两个实根一个大于k一个小于k：

(7)方程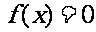有两个实根都在区间[m,n]内：

(8)方程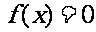有两个实根，只有一个在区间[m,n]内：

二次函数的解析式的三种形式：

一般式：

顶点式：

两根式：

二次函数、一元二次方程及一元二次不等式之间的关系．

思考;

3. 二次函数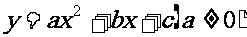在指定区间[m,n]上的最值问题：(轴定区间动；轴动区间定)

25．某商店经营一批进价为10元的商品，据市场分析，每件售价15元，则一天可售55

件，如果售价每降1元，则日销售量可增加3件，(为了方便结账，定价取整数)设销售单价为x元，日销售量为y件，日获利为w元。

解答下列问题：

(1)　　　 试写出y与x之间的函数关系式；

(2)　　　 试写出w与x之间的函数关系式；

(3)　　　 计算单价为12元时的日销售量和日是售利润；

(4)　　　 若使日销售利润达到200元，且老板要尽快减少库存，则售价应定为多少元?

(5)　　　 在如图所示的坐标系内作出w与x的图象，观察图象，说明定价为多少元时，日获利最多，为多少？

(6)　　　 若物价局限定其定价不能超过其进价的80%，则定价为多少元时，可获最大利润？

(7)　　　 试问：在(5)的条件下，销售利润是否有最小值？若有，试求出，若无，说明理由；

(8)　　　 分别写出本题中w与x的取值范围。

24．某摩托车生产企业，上年度生产摩托车的投入成本为1万元/辆，出厂价为1.2万元/辆，年销售量为1000辆，本所度为适应市场需求，计划提高产品档次，适度增加投入成本，若每辆车投入成本增加的比例为x(0＜x＜1)，则出厂价相应增加的比例为0.75x，同时预测年销售量增加的比例为0.6x，已知年利润=(出厂价－投入成本)×年销售量。

(1)　　　　　　　　　　　 写出本年度预计的年利润y与投入成本增加的比例x的关系式；

(2)　　　　　　　　　　　 为使本年度的年利润比上年度有所增加，问投入的成本比例x应在什么范围内？

23．启明公司生产某种产品，每件产品成本是3元，售价是4元，年销售量是10万件。为了获得更好的效益，公司准备拿出一定的资金做广告，根据经验，每年投入的广告费是x(万元)时，产品的啊销售量将是原销售量的y倍，且y=-1/10X²+7/10X+7/10，如果把利润看作是销售总额减去成本费和广告费：

(1)　　　 试写出年利润S(万元)与广告费x(万元)的函数关系式，并计算广告费是多少元时，公司获得的年利润最大，最大年利润是多少万元；

(2)　　　 把(1)中的最大利润留出3万元作广告，其余的资金投资新项目，现有6个项目可供选择，各项目每股投资额和预计年收益如下表：

如果每个项目只能投一股，且要求所有投资项目的收益总额不得低于1.6万元，问有几种符合要求的投资方式？写出每种投资方式所选的项目。

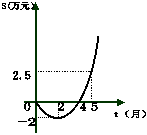
22．某公司推出了一种高效环保洗涤用品，年初上市后，公司经历了从亏损到盈利的过程，下面的二产供销函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s 与t之间的关系)。

根据图象提供的信息，解答下列问题：

(1)　　　 由已知图象上的三点坐标，求累积利润s(万元)与销售时间t(月)之间的关系式；

(2)　　　 求截止到几个月末公司累积利润可达到30万元；

(3)　　　 求第8个月公司所获利润是多少万元？