
2、已知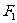 ,
,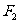 椭圆
椭圆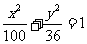 的两个焦点,P(
的两个焦点,P(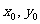 )为椭圆上一点,
)为椭圆上一点,
当 <0时,
<0时,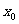 的取值范围为_________.。
的取值范围为_________.。
1、平面直角坐标系中,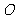 为坐标原点,已知
为坐标原点,已知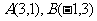 ,若点
,若点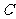 满足
满足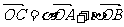 ,其中
,其中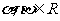 ,且
,且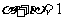 ,则点
,则点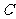 的轨迹方程为( )
的轨迹方程为( )
A. 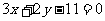 B.
B. 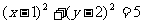
C. 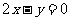 D.
D. 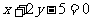
3、运用平面向量综合知识,探求动点轨迹方程,还可再进一步探求曲线的性质。
例2.已知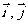 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设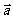 =
=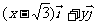 ,
, 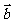 =
=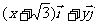 ,且满足|
,且满足|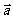 |+|
|+|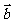 |=4.
|=4.
⑴求点P(x,y)的轨迹C的方程.
⑵如果过点Q(0,m)且方向向量为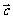 =(1,1) 的直线l与点P的轨迹交于A,B两点,当
=(1,1) 的直线l与点P的轨迹交于A,B两点,当 AOB的面积取到最大值时,求m的值。
AOB的面积取到最大值时,求m的值。
解:(1)
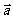 =
=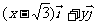 , |
, |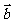 |=
|=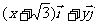 ,且|
,且|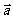 |+|
|+|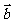 |=4.
|=4.
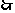 点P(x,y)到点(
点P(x,y)到点(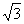 ,0),(-
,0),(-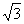 ,0)的距离这和为4,故点P的轨迹方程为
,0)的距离这和为4,故点P的轨迹方程为
(2)设A(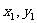 ),B(
),B(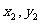 )依题意直线AB的方程为y=x+m.代入椭圆方程,得
)依题意直线AB的方程为y=x+m.代入椭圆方程,得 ,则
,则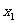 +
+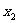 =-
=-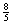 m,
m, 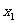

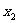 =
=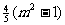
因此,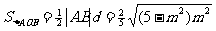
当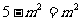 时,即m=
时,即m=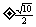 时,
时,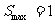
[变式1] 已知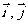 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设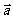 =
=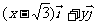 ,
, 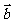 =
=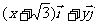 ,且满足||
,且满足||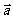 |-|
|-|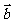 ||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)
||=2.求点P(x,y)的轨迹C的方程.(轨迹为双曲线)
[变式2] 已知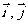 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设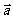 =
=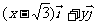 ,
, 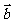 =
=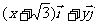 ,且满足
,且满足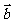

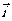 =|
=|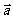 |.求点P(x,y)的轨迹C的方程.
|.求点P(x,y)的轨迹C的方程.
[提示:设K(-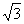 ,0),F (
,0),F (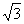 ,0),则
,0),则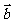

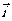 表示
表示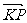 在x轴上射影,即点P到x= -
在x轴上射影,即点P到x= -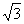 的距离,所以点P到定点F的距离与到定直线x= -
的距离,所以点P到定点F的距离与到定直线x= -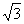 的距离比为1,故点P的轨迹是以(
的距离比为1,故点P的轨迹是以(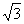 ,0)为焦点以x= -
,0)为焦点以x= -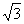 为准线抛物线]
为准线抛物线]
巩固训练
2.运用向量的数量积处理解几中有关长度、角度、垂直等问题
 例2如图,点F(a,0)(a>0),点P 在y轴上运动,点M在x轴上运动,点N为动点,且
例2如图,点F(a,0)(a>0),点P 在y轴上运动,点M在x轴上运动,点N为动点,且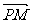 ·
·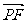 =0,
=0,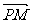 +
+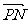 =0。
=0。
(1)求点N的轨迹C的方程;
(2)过点F(a ,0)的直线l(不与x轴垂直)与曲线C交于A、B两点,设点K(-a,0),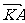 与
与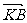 的夹角为θ,
的夹角为θ,
求证:0<θ<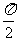 .
.
[分析] (1)分别设出P、M与N点的坐标,将已知向量坐标化,然后利用向量数量积及向量相等知识找到等量关系。
(2)利用向量的夹角公式可知,要证0<θ<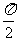 ,只要证
,只要证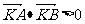 。
。
[解析] (1)y2=4ax
(2) 证明:设AB的方程为y=k(x-a),代入y2=4ax得
k2x2-2a(k2+2)x+k2a2=0
设A(x1 , y1)、B(x2 , y2),则
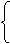 x1+x2=
x1+x2=
x1 x2=a2
∵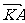 =(x1+a , y1),
=(x1+a , y1), 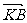 =(x2+a , y2)
=(x2+a , y2)
∴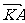 ·
·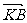 =(x1+a)(x2+a)+y1 y2
=(x1+a)(x2+a)+y1 y2
=x1x2+a ( x1+x2)+a2+(-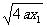 ) · (
) · (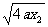 )
)
=a2+a·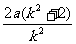 + a2-4a2=
+ a2-4a2= >0,
>0,
∵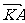 与
与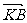 的夹角为θ,
的夹角为θ,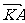 与
与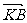 不共线,
不共线,
∴θ≠0,∴cosθ= >0 , 即0<θ<
>0 , 即0<θ<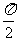 .
.
变式:给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求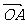 与
与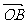 夹角的大小;
夹角的大小;
[解答] (Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为
y=x-1,将y=x-1代入方程y2=4x,并整理得x2-6x+1=0
设A(x1,y1),B(x2,y2),则有x1+x2=6, x1x2=1,
从而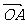 ·
·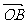 =x1x2+y1y2=2x1x2-(x1+x2)+1=-3
=x1x2+y1y2=2x1x2-(x1+x2)+1=-3
︱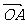 ︱·︱
︱·︱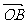 ︱=
︱=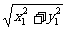 ·
·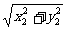 =
=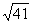 ,
,
cos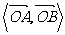 =
=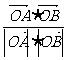 =
=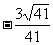
所以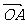 与
与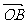 夹角的大小为π-arcos
夹角的大小为π-arcos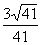 .
.
1.运用向量共线的充要条件处理解几中有关平行、共线等问题
运用向量共线的充要条件来处理解几中有关平行、共线等问题思路清晰,易于操作,比用斜率或定比分点公式研究这类问题要简捷的多。
例1.已知椭圆的中心为坐标原点O,焦点在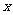 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,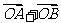 与
与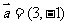 共线。
共线。
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且 ,证明
,证明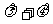 为定值。
为定值。
解:设椭圆方程为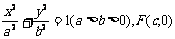
则直线AB的方程为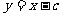 ,代入
,代入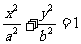 ,化简得
,化简得
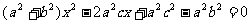 .
.
令A(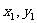 ),B
),B ),则
),则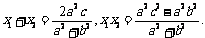
由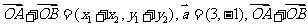 与
与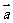 共线,得
共线,得
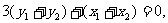 又
又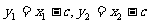 ,
,
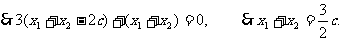
即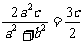 ,所以
,所以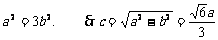 ,
,
故离心率
(II)证明:(1)知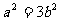 ,所以椭圆
,所以椭圆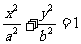 可化为
可化为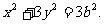
设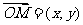 ,由已知得
,由已知得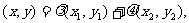
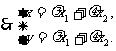
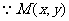 在椭圆上,
在椭圆上,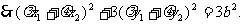
即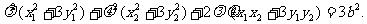 ①
①
由(1)知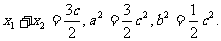

又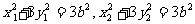 ,代入①得
,代入①得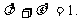
故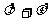 为定值,定值为1.
为定值,定值为1.
变式:椭圆的中心是原点O,它的短轴长为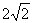 ,相应于焦点F(c, 0)(c>0)的准线l与x轴相交于点A,
,相应于焦点F(c, 0)(c>0)的准线l与x轴相交于点A,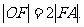 ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)若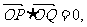 ,求直线PQ的方程;
,求直线PQ的方程;
(Ⅲ)设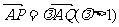 ,过点P且平行于准线l的直线与椭圆相交于另一点M,
,过点P且平行于准线l的直线与椭圆相交于另一点M,
证明:
[简解] (Ⅰ) 椭圆方程为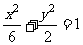 ,离心率
,离心率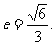 (Ⅱ)略.
(Ⅱ)略.
(Ⅲ) [证明] 设P(x1,y1),Q (x2,y2),又A(3,0),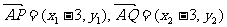 由已知得方程组:
由已知得方程组:
 ;
; 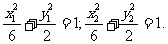
注意λ>1,消去x1、y1和y2 得
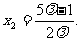 因F(2 , 0), M(x1,-y1),
因F(2 , 0), M(x1,-y1),
故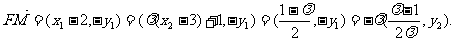
而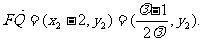
所以
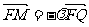 .
.
4.平面向量作为工具综合处理有关长度、角度、垂直、射影等问题以及圆锥曲线中的典型问题。
引入:平面几何与解析几何的结合通常涉及到夹角、平行、垂直、共线、轨迹等问题的处理,解决此类问题基本思路是将几何问题坐标化、符号化、数量化,从而将推理转化为运算;或者考虑向量运算的几何意义,利用其几何意义解决有关问题。主要包括以下三种题型:
例题讲解
3.直线与圆锥曲线的位置关系问题(交点、弦长、中点弦与斜率、对称问题)确定参数的取值范围;
2.椭圆、双曲线、抛物线的定义及简单几何性质的灵活运用;
1.向量的概念、向量的加法和减法、实数与向量的积、两个向量共线的充要条件、平面向量的数量积及其几何意义、平面两点间的距离公式、线段定比分点人坐标公式和向量的平移公式;
3、情感、态度与价值观目标:
帮助学生体会形数的统一美,激发学生的学习兴趣,培养学生辩证唯物主义世界观;通过知识间的相互融合,培养学生的创新意识。
教学重点:理解并能灵活运用平面向量的解决圆锥曲线的基本问题。
教学难点:平面向量与解析几何的内在联系和知识综合,选择适当的方法解决解析几何的综合问题。
教学方法:讲练结合,探究式教学,反思教学。
教学准备:多媒体电脑、课件等。
教学立意:
平面向量是高中数学新增内容,它具有代数形式和几何形式的双重身份,是数形结合的典范,能与中学数学内容的许多主干知识综合,形成知识交汇点。基于高考数学重视能力立意,在知识网络的交汇点上设计试题,平面向量与解析几何融合交汇的试题便应运而生,试题以解析几何为载体,以探讨直线和圆锥曲线的位置关系为切入点,以向量为工具,着重考查解析几何中的基本的数学思想方法和综合解题能力。
本专题就以下三方面对平面向量与圆锥曲线交汇综合的问题进行复习:㈠运用向量共线的充要条件处理解几中有关平行、共线等问题;㈡运用向量的数量积处理解几中有关长度、角度、垂直等问题;㈢运用平面向量综合知识,探求动点轨迹方程,还可再进一步探求曲线的性质。
教学过程
基础知识梳理:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com