
3.已知:P为Rt△ABC所在平面外一点,∠ACB=90°,P到直角顶点C的距离等于24,P到平面ABC的距离等于12,P到AC
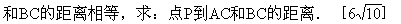
2.已知:AB是平面α的一斜线,B为斜足,AB=a.直线AB与平面α所成的角等于θ,AB在平面α内的射影A1B与平面α内过B

1.已知:∠BSC=90°,直线SA∩平面BSC=S.∠ASB=∠ASC=60°,求:SA和平面BSC所成角的大小.[45°]
4.了解课本第33页第11题.
教学重点和难点
教学的重点是进一步掌握三垂线定理及其逆定理并应用它们来解有关的题.教学的难点是在讲公式cosθ1·cosθ2=cosθ应用时比较θ2与θ的大小.
教学设计过程
师:上一节课我们讲了三垂线定理及其逆定理的证明并初步应用了这两个定理来解一些有关的题.今天我们要进一步应用这两个定理来解一些有关的题,先看例1.
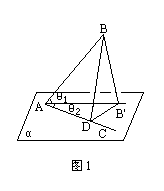
例1 如图1,AB和平面α所成的角是θ1;AC在平面α内,BB′⊥平面α于B′,AC和AB的射影AB′成角θ2,设∠BAC=θ.求证:
cosθ1·cosθ2=cosθ.
师:这是要证明三个角θ1,θ2和θ的余弦的关系,θ1已经在直角△ABB′中,我们能否先作出两个直角三角形分别使θ2和θ是这两个直角三角形中的锐角.
生:作B′D⊥AC于D,连BD,则BD⊥AC于D.这时θ2是直角△B′DA中的一个锐角,θ是直角△ABD中的一个锐角.
师:刚才的表述是应用三垂线定理及其逆定理时常常使用的“套话”,我们一定要很好理解并能熟练地应用.现在已经知道θ1、θ2和θ分别在三个直角三角形中,根据三角函数中的余弦的定义分别写出这三个角的余弦,再来证明这公式.
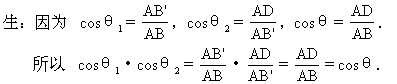
师:这个公式的证明是利用余弦的定义把它们转化成邻边与斜边的比,为此要先作出直角三角形,为了作出直角三角形我们应用了三垂线定理.当然也可用它的逆定理.
这个公式是在课本第121页总复习参考题中的第3题.我们为什么要提前讲这个公式呢?讲这个公式的目的是为了用这个公式,因为在解许多有关题时都要用到这公式.那我们要问在什么条件下可用这个公式?
生:因为θ1是斜线AB与平面α所成的角,所以只有当图形中出现斜线与平面所成的角时,才有可能考虑用这公式.
师:为了在使用这个公式时方便、易记,我们规定θ1表示斜线与平面所成的角,θ2是平面内过斜足的一条射线与斜线射影所成的角,θ是这条射线与斜线所成的角.下面我们来研究一下这个公式的应用.
应用这个公式可解决两类问题.
第一是求值.即已知这公式中的两个角,即可求出第三个角或其余弦值.
例如:
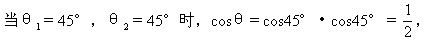
θ=60°,这时θ2<θ;

当θ1=45°,θ2=135°时,cosθ=cos45°·cos135°=
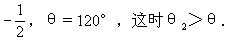
第二是比较θ2与θ的大小.因为我们已经规定θ1是斜线与平面所成的角,一定有0°<θ1<90°,它的大小不变,为了比较θ2与θ的大小,下面分三种情况进行讨论.
(1)θ2=90°,因为θ2=90°,所以cosθ2=0,因此cosθ=cosθ1·cosθ2=0,故θ=90°.当θ=90°时,我们也可以证明θ2=90°.
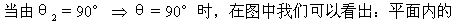
一条直线如果和斜线的射影垂直,那么它就和斜线垂直.这就是三垂线定理.
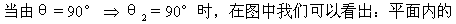
一条直线如果和斜线垂直,那么它就和斜线的射影垂直.这就是三垂线定理的逆定理.
所以,我们可以这样说,这个公式是三垂线定理及其逆定理的一般情况,而三垂线定理及其逆定理是这公式的特殊情况.
现在我们来研究在θ2是锐角时,θ2与θ的大小.
(2)0°<θ2<90°.
师:在这个条件下,我们怎样来比较θ2与θ的大小?
生:因为0°<θ1<90°,所以0<cosθ1<1,又因为0°<θ2<90°,所以0<cosθ2<1.又因为cosθ=cosθ1·cosθ2,所以0<cosθ1<1,而且cosθ=cosθ1·cosθ2<cosθ2,在锐角条件下,余弦函数值大的它所对应的角小.所以θ2<θ.
师:现在我们来讨论当θ2是钝角时,θ2与θ的大小.
(3)90°<θ2<180°.
在这个条件下,我们不再用公式cosθ1·cosθ2=cosθ做理论上的证明来比较θ2与θ的大小,而是一起来看模型(或图形).
我们假设θ2的邻补角为θ′2,θ的邻补角为θ′,即θ2+θ′2=180°,θ+θ′=180°.在模型(或图形)中我们可以看出当θ2是钝角时,θ也是钝角,所以它们的两个邻补角θ′2和θ′都是锐角,由对第二种情况的讨论我们知道θ′2<θ′.由等量减不等量减去小的大于减去大的,所以由θ2=180°-θ′2,θ=180°-θ′,可得θ2>θ.
根据以上讨论现在小结如下:
当θ2=90°时,θ=θ2=90°,它们都是直角.
当0°<θ2<90°时,θ2<θ,它们都是锐角;
当90°<θ2<180°时,θ2>θ,它们都是钝角.
关于公式cosθ1·cosθ2=cosθ的应用,今后还要随着课程的进展而反复提到.现在我们来看例2.
例2 如图2,在正方体ABCD-A1B1C1D1中,求证:
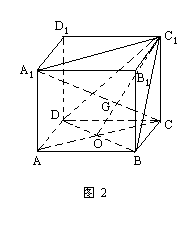
(1)A1C⊥平面C1DB于G;
(2)垂足G为正△C1DB的中心;
(3)A1G=2GC.
师:我们先来证明第(1)问.要证直线与平面垂直即要证什么?
生:要证A1C与平面C1DB内两条相交的直线垂直.
师:我们先证A1C为什么与DB垂直?
生:连AC,对平面ABCD来说,A1A是垂线,A1C是斜线,AC是A1C在平面ABCD上的射影,因为AC⊥DB(正方形的性质),所以 A1C⊥DB.(三垂线定理)
同理可证A1C⊥BC1.
因为A1C⊥平面C1DB(直线与平面垂直的判定理)
(在证A1C⊥BC1时,根据情况可详、可略,如果学生对应用三垂线定理还不太熟悉,则可让学生把这证明过程再叙述一遍,因为这时是对平面B1BCC1来说,A1B1是垂线,A1C是斜线,B1C是A1C在平面B1BCC1上的射影,由B1C⊥BC1,得A1C⊥BC1)
师:现在来证第(2)问,垂足G为什么是正△C1DB的中心?
生:因为A1B=A1C1=A1D,所以BG=GC1=DG,故G是正△C1DB的外心,正三角形四心合一,所以G是正△C1DB的中心.
师:现在来证第(3)问,我们注意看正方体的对角面A1ACC1,在这对角面内有没有相似三角形?
生:在正方体的对角面A1ACC1内,由平面几何可知△A1GC1∽△OGC,且A1C1∶OC=A1G∶GC,所以A1G∶GC=2∶1,因此A1G=2GC.
师:例2是在正方体的体对角线与其异面的面对角线互相垂直引申而来,而例2也是一个基本的题型,对于以后证有关综合题型时很有用.所以对例2的证明思路和有关结论,尽可能的理解、记住.现在我们来看例3.
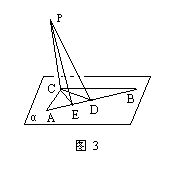
例3 如图3,已知:Rt△ABC在平面α内,PC⊥平面α于C,D为斜边AB的中点,CA=6,CB=8,PC=12.求:
(1)P,D两点间的距离;
(2)P点到斜边AB的距离.
师:现在先来解第(1)问,求P,D两点间的距离.

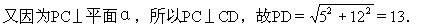
师:现在我们来解第(2)问,求P点到AB边的距离.
生:作PE⊥AB于E,连CE则CE⊥AB.(三垂线定理的逆定理)PE就是P点到AB边的距离.
师:要求PE就要先求CE,CE是直角三角形ABC斜边上的高,已知直角三角形的三边如何求它斜边上的高呢?
生:可用等积式CE·AB=AC·CB,即斜边上的高与斜边的乘积等于两直角边的乘积.
师:这个等积式是怎样证明的?
生:有两种证法.因CE·AB是Rt△ABC面积的二倍,而AC·CB也是Rt△ABC面积的二倍,所以它们相等;也可用△BCE∽△ABC,对应边成比例推出这个等积式.
师:这个等积式很有用,根据这个等积式,我们可以由直角三角形的三边求出斜边上的高,这个等积式以后在求有关距离问题时会常常用到,所以要理解、记住、会用.现在就利用这等积式先求CE,再求PE.
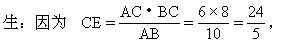

师:通过这一题我们要区分两种不同的距离概念及求法;在求点到直线距离时,经常要用到三垂线定理或其道定理;在求直角三角形斜边上的高时会利用上述的等积式来求斜边上的高.现在我们来看例4.
例4 如图4,已知:∠BAC在平面α内,PO 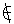 α,PO⊥平面α于O.如果∠PAB=∠PAC.
α,PO⊥平面α于O.如果∠PAB=∠PAC.
求证:∠BAO=∠CAO.
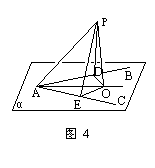
(这个例题就是课本第32页习题四中的第11题.这个题也可以放在讲完课本第30页例1以后讲.不论在讲课本第30页例1,还是在讲这个例时,都应先用模型作演示,使学生在观察模型后,得出相关的结论,然后再进行理论上的证明,这样使学生对问题理解得具体、实在,因而效果也较好)
师:当我们观察了模型后,很容易就猜想到了结论.即斜线PA在平面α上的射线是∠BAC的角平分线所在的直线,现在想一想可以有几种证法?
生:作OD⊥AB于D,作OE⊥AC于E,连PD,PE,则PD⊥AB,PE⊥AC.
所以Rt△PAD≌Rt△PAE,因此PD=PE,故OD=OE,所以∠BAO=∠CAO.
师:今天我们讲了公式cosθ1·cosθ2=cosθ.能否用这公式来证明这题.
(利用这公式来证明这个题,完全是由学生想到的,当然如果有的班学生成绩较差,思路不活,也可做些必要的提示)
生:因为∠PAO是斜线与平面α所成的角,所以可以考虑用公式cosθ1·cosθ2=cosθ.∠PAO相当于θ1;∠PAB=∠PAC它们都相当于θ,由公式可得θ2=θ′2,即∠BAO=∠CAO.
师:今天我们是应用三垂线定理及其逆定理来解这四个例题.例1、例2、例4是三个基本题.对这三个题一定要会证、记住、会用.关于这三个题的应用,以后还会在讲课过程中反复出现.在高考题中也曾用到.
作业
课本第33页第13题.
补充题
3.理解正方体的体对角线与其异面的面对角线互相垂直及其应用;
2.理解公式cosθ1·cosθ2=cosθ的证明及其初步应用;(课本第122页第3题)
1.进一步理解、记忆并应用三垂线定理及其逆定理;
18.(1)由
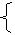 |
y=x-a, |
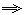 x2-2(a+p)x+a2=0. x2-2(a+p)x+a2=0. |
|
y2=2px |
由弦长公式得|AB|=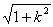 |x2-x1|=
|x2-x1|=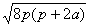 .
令0<
.
令0<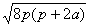 ≤2p,
则-(p/2)<a≤-(p/4).
(2)设AB的垂直平分线交AB于Q点,Q(x3,y3)、A(x1,y1)、B(x2,y2),则
≤2p,
则-(p/2)<a≤-(p/4).
(2)设AB的垂直平分线交AB于Q点,Q(x3,y3)、A(x1,y1)、B(x2,y2),则
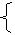 |
x3=(x1+x2)/2=a+p, |
|
y3=(y1+y2)/2=p, |
∴ |QM|2=2p2.
∵ △MNQ为等腰直角三角形,
∴ |QN|=|QM|=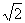 p.
S△NAB=(1/2)|AB|·|NQ|=(
p.
S△NAB=(1/2)|AB|·|NQ|=(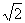 /2)p|AB|≤
/2)p|AB|≤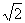 p2.
即△NAB面积的最大值为
p2.
即△NAB面积的最大值为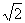 p2.
19.设满足条件的双曲线存在,则
(1)若双曲线焦点在x轴上,
∵ 渐近线为y=±(1/2)x,
∴ 可设双曲线方程为(x2/4b2)-(y2/b2)=1(b>0).
?设动点P为(x,y),则
|AP|=
p2.
19.设满足条件的双曲线存在,则
(1)若双曲线焦点在x轴上,
∵ 渐近线为y=±(1/2)x,
∴ 可设双曲线方程为(x2/4b2)-(y2/b2)=1(b>0).
?设动点P为(x,y),则
|AP|=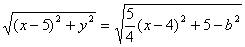 ,
且x∈(-∞,-2b]∪[2b,+∞).
若2b≤4,则当x=4时,|AP|min=
,
且x∈(-∞,-2b]∪[2b,+∞).
若2b≤4,则当x=4时,|AP|min=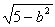 =
=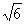 ,此时b2=-1,无解;
若2b>4,则当x=2b时,|AP|min=|2b-5|=
,此时b2=-1,无解;
若2b>4,则当x=2b时,|AP|min=|2b-5|=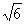 ,解得b=(5±
,解得b=(5±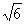 )/2,但(5-
)/2,但(5-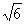 /2)<2应舍去.
则存在双曲线(x2/(5+
/2)<2应舍去.
则存在双曲线(x2/(5+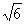 )2)-(y2/((5+
)2)-(y2/((5+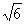 )/2)2)=1符合条件.
(2)若双曲线焦点在y轴上,则可设双曲线方程为(y2/b2)-(x2/4b2)=1(b>0).设P(x,y),则
|AP|=
)/2)2)=1符合条件.
(2)若双曲线焦点在y轴上,则可设双曲线方程为(y2/b2)-(x2/4b2)=1(b>0).设P(x,y),则
|AP|= (x∈R).
∵ x∈R,∴ 当x=4时,|AP|min=
(x∈R).
∵ x∈R,∴ 当x=4时,|AP|min=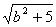 =
=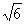 .?
∴b2=1,则此时存在双曲线y2-(x2/4)=1满足题设条件.
.?
∴b2=1,则此时存在双曲线y2-(x2/4)=1满足题设条件.
20.(1)由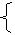 |
y=xtgθ, |
解得点A的坐标为 |
|
(x2/m2)+(y2/n2)=1 |
x=mn/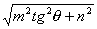 ,y=mntgθ/
,y=mntgθ/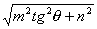 .
∴ S=4|xy|=(4m2n2tgθ)/(m2tg2θ+n2).
(2)∵ S=(4m2n2)/(m2tgθ+(n2/tgθ)),
①当m>n,即(n/m)<1时,当且仅当tg2θ=(n2/m2)时,S≤(4m2n2)/(2mn)=2mn.
由于θ∈(0,(π/4)],?∴0<tgθ≤1,故取tgθ=(n/m),Smax=2mn,?∴u=2mn.?
②当m<n,即(n/m)>1时,易证S在θ∈(0,(π/4)]上为增函数,故取θ=(π/4),即tgθ=1时,Smin=(4m2n2)/(m2+n2).
.
∴ S=4|xy|=(4m2n2tgθ)/(m2tg2θ+n2).
(2)∵ S=(4m2n2)/(m2tgθ+(n2/tgθ)),
①当m>n,即(n/m)<1时,当且仅当tg2θ=(n2/m2)时,S≤(4m2n2)/(2mn)=2mn.
由于θ∈(0,(π/4)],?∴0<tgθ≤1,故取tgθ=(n/m),Smax=2mn,?∴u=2mn.?
②当m<n,即(n/m)>1时,易证S在θ∈(0,(π/4)]上为增函数,故取θ=(π/4),即tgθ=1时,Smin=(4m2n2)/(m2+n2).
所以u=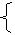 |
2mn(0<n<m), |
|
(4m2n2)/(m2+n2)(0<m<n). |
(3)当(m/n)>1时,u>mn恒成立;
当(m/n)<1时,由(4m2n2)/(m2+n2)>mn,得
(m/n)2-4(m/n)+1<0,解得2-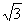 <(m/n)<1.
综上所述,当u>mn时,(m/n)∈(2-
<(m/n)<1.
综上所述,当u>mn时,(m/n)∈(2-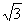 ,1)∪(1,+∞).
,1)∪(1,+∞).
3.、棱长为1的正方体ABCD-A1B1C1D1中,AC与BD交于点E,CB与CB1交于点F.
(I)求证:A1C⊥平面BDC1;
(II)求二面角B-EF-C的大小的余弦值。
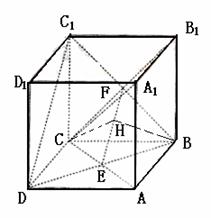 解法一:(Ⅰ)∵A1A⊥底面ABCD,则AC是A1C在底面ABCD的射影.
解法一:(Ⅰ)∵A1A⊥底面ABCD,则AC是A1C在底面ABCD的射影.
∵AC⊥BD.∴A1C⊥BD.
同理A1C⊥DC1,又BD∩DC1=D,
∴A1C⊥平面BDC1.
(Ⅱ)取EF的中点H,连结BH、CH,

又E、F分别是AC、B1C的中点,

解法二:(Ⅰ)以点C为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0).
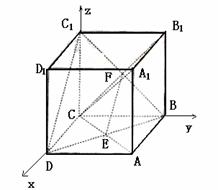 D(1,0,0),B(0,1,0),A1(1,1,1),C1(0,0,1),D1(1,0,1)
D(1,0,0),B(0,1,0),A1(1,1,1),C1(0,0,1),D1(1,0,1)

(Ⅱ)同(I)可证,BD1⊥平面AB1C.

2、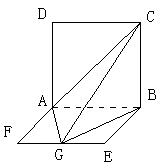 如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 G是EF的中点,
G是EF的中点,
(Ⅰ)求证平面AGC⊥平面BGC;
(Ⅱ)求GB与平面AGC所成角的正弦值.
(Ⅲ)求二面角B-AC-G的大小.
解析:如图,以A为原点建立直角坐标系,
则A(0,0,0),B(0,2a,0),C(0,2a,2a ),
G(a,a,0),F(a,0,0)
(I)证明:略.
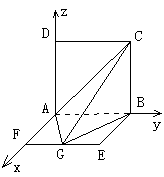 (II)由题意可得
(II)由题意可得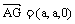 ,
,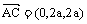 ,
,
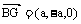 ,
,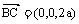 ,
,
设平面AGC的法向量为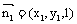 ,
,
由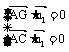
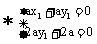
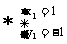
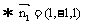
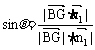
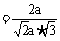
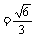
(III)因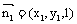 是平面AGC的法向量,
是平面AGC的法向量,
又AF⊥平面ABCD,平面ABCD的法向量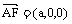 ,得
,得
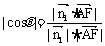
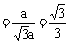 , ∴ 二面角B-AC-G的大小为
, ∴ 二面角B-AC-G的大小为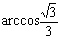 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com