
(二)选做题(13-15题,考生只能从中选做两题)
13.  .
.
[解析]由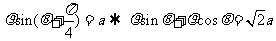 ,化为直角坐标方程为
,化为直角坐标方程为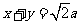 ,圆
,圆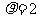
化为直角坐标方程为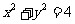 ,由圆的弦长公式
,由圆的弦长公式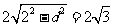 ,得
,得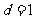 ,即
,即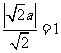 ,故
,故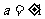 .
.
[链接高考]本小题主要考查直线和圆的极坐标方程与直角坐标方程的互化,以及利用圆的几何性质计算圆的弦长等基本方法,我们要给予重视.
14.  .
.
[解析]由柯西不等式的二维形式,得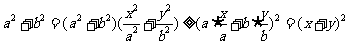 .
.
[链接高考]本小题主要考查柯西不等式的应用,拼凑成柯西不等式的结构形式是解题的关键.
15.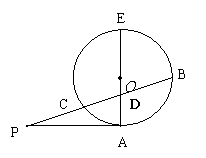
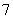 .
.
[解析]如图,连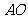 并延长,交圆
并延长,交圆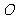 与另一点
与另一点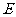 ,交割线
,交割线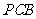 于点
于点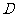 ,
,
则RtΔ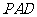 中,由
中,由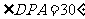 ,
,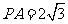 ,得
,得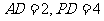 ,而
,而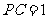 ,
,
故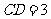 ,由切割线定理,得
,由切割线定理,得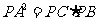 ,即
,即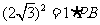 ,则
,则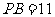 ,
,
故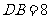 .设圆
.设圆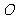 的半径为
的半径为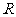 ,由相交弦定理,
,由相交弦定理,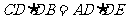 ,即
,即
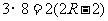 ,得
,得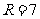 .
.
[链接高考]本小题主要考查圆的切割线定理和相交弦定理.
(一)必做题(9-12题)
9. 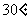 .
.
[解析]如图,设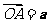 ,
,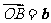 ,则
,则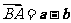 ,
, ,
,
由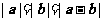 知Δ
知Δ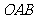 为菱形,故
为菱形,故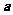 与
与 的夹角为
的夹角为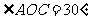 .
.
[链接高考]平面向量在高考一般有一道选择或填空题,也可能与三角、解几在解答题中综合考查.
本小题灵活利用向量加法和减法的几何意义来求解,直观、简捷,避免了繁杂的计算.
10. 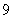 .
.
[解析]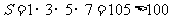 ,故输出
,故输出 .
.
[链接高考]算法和程序框图在近两年的广东高考都有考查,复习中要给予高度重视.
11.  .
.
[解析]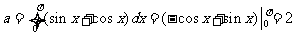 ,二项式
,二项式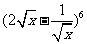 的通项公式为
的通项公式为
 ,令
,令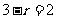 ,得
,得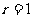 ,故展开式中含
,故展开式中含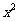 项的系数是
项的系数是
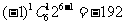 .
.
[链接高考]本小题设计巧妙,综合考查定积分和二项式定理,是一道以小见大的中档题,不可小视!
12. 底面边长和侧棱长都确定的底面上任意一点到三个侧面的距离之和为定值..
[解析]设等腰三角形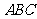 的底边
的底边 和腰
和腰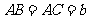 确定,则它的高
确定,则它的高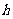 确定,设
确定,设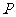 是底边
是底边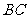 上任一点,
上任一点,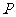 到两腰的距离分别为
到两腰的距离分别为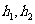 ,由面积分割得:
,由面积分割得: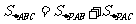 ,即
,即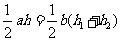 ,故
,故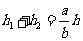 为定值.
为定值.
类似地,设正三棱锥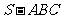 的底面边长和棱长确定,则它的高
的底面边长和棱长确定,则它的高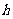 确定,底面积
确定,底面积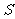 确定,一个侧面的面积
确定,一个侧面的面积 也确定,设
也确定,设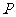 是底面
是底面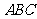 上任一点,
上任一点,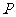 到到三个侧面的距离分别为
到到三个侧面的距离分别为 ,由体积分割得:
,由体积分割得: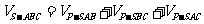 ,即
,即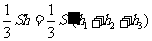 ,故
,故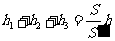 为定值.
为定值.
[链接高考]本小题是一道类比推理问题,主要考查创新思维能力. 事实上,平面几何中的不少定理、结论都可以类比推广到空间中去,值得我们进一步去探索和研究.
8.D.
[解析]如图,易得答案选D.
[链接高考]本题通过简单的线性规划问题,考查化归
转化和数形结合思想.
7.A.
[解析]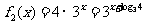 ,
,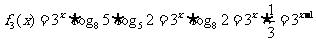 ,故
,故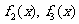
的图象可分别由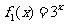 的图象向左平移
的图象向左平移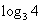 个单位、向右平移1个单位得到.
个单位、向右平移1个单位得到.
 [链接高考]本小题是一道新定义类型的创新题,主要考查函数的图象变换以及指数、对数的运算,考生容易错选C,问题出在对数的运算性质不熟练.
[链接高考]本小题是一道新定义类型的创新题,主要考查函数的图象变换以及指数、对数的运算,考生容易错选C,问题出在对数的运算性质不熟练.
6.B.
[解析]依题意,使用的这台仪器的日平均耗资为
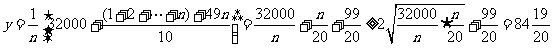 ,等号当且仅当
,等号当且仅当
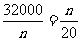 ,即
,即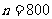 时取得.
时取得.
[链接高考]本小题是一道与生活实际紧密相关的应用题,考查等差数列的求和以及灵活运用均值不等式解决问题的能力.
5.D.
[解析]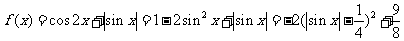 ,注意到
,注意到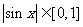 ,
,
故当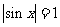 时,
时,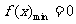 ;当
;当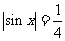 时,
时,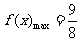 ,因此
,因此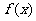 的值域为
的值域为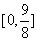 .
.
[链接高考]本小题考查简单的三角变换和二次函数的最值等知识,属于基础题.
4.B.
[解析]若甲是主犯,则乙、丙都说真话,甲、丁都说假话,不合题意.若乙是主犯,则甲、乙、丁都说假话,丙说真话,符合题意.
[链接高考]本小题情境通俗易懂,主要考查逻辑思维和推理能力,难度不大.
3.C.
[解析]频率为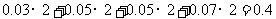 ,∴所求人数为
,∴所求人数为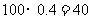 .
.
[链接高考]频率分布直方图是高考新增的考点,难度不高,但必须掌握相关的概念.
2. A.
[解析]依题意,知这个几何体是底面直径和高都为1的圆柱,故其体积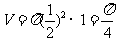 .
.
[链接高考]三视图是新课标新增的内容,近两年的广东高考试题中都有考查,一般都比较基础,
要力求“稳拿”.
1. A.
[解析]由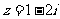 ,则
,则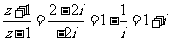 .
.
[链接高考]本小题考查复数的基本运算,属于送分题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com