
4、在△ABC中,BC=3,AB=2,且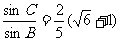 ,A= 。
,A= 。
3、在△ABC中,sinA=2cosBsinC,则三角形为 。
2、在△ABC中,若a2>b2+c2,则△ABC为;若a2=b2+c2,则△ABC为 ;
若a2<b2+c2且b2<a2+c2且c2<a2+b2,则△ABC为 。
1、在△ABC中,bcosA=acosB,则三角形为( )
A.直角三角形 B.锐角三角形 C.等腰三角形?D.等边三角形
22.某公司决定给员工增加工资,提出了两个方案,让每位员工自由选择其中一种.甲方案是:公司在每年年末给每位员工增资1000元;乙方案是每半年末给每位员工增资300元.某员工分别依两种方案计算增资总额后得到下表:
|
工作年限 |
方案甲 |
方案乙 |
最终选择 |
|
1 |
1000 |
600 |
方案甲 |
|
2 |
2000 |
1200 |
方案乙 |
|
≥3 |
|
|
方案甲 |
(说明:①方案的选择应以让自己获得更多增资为准. ②假定员工工作年限均为整数.)
(1)他这样计算增资总额,结果对吗?如果让你选择,你会怎样选择增资方案?说明你的理由;
(2)若保持方案甲不变,而方案乙中每半年末的增资数改为a元,问:a为何值时,方案乙总比方案甲多增资?
21.已知数列{an}满足a1=4,an=4-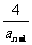 (n≥2),令bn=
(n≥2),令bn=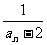 .
.
(1)求证数列{bn}是等差数列;
(2)求数列{an}的通项公式.
20.设函数 ,数列
,数列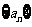 的通项
的通项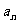 满足
满足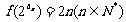 .
.
(1)求数列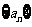 的通项公式;
的通项公式;
(2)判定数列{a n }的单调性.
19.数列{an}是首项为23,公差为整数的等差数列,且第六项为正,第七项为负.
(1)求数列的公差;
(2)求前n项和Sn的最大值;
(3)当Sn>0时,求n的最大值.
18.在数列{an}中,a1=2,a17=66,通项公式是项数n的一次函数.
(1)求数列{an}的通项公式; 
(2)88是否是数列{an}中的项.

17.已知关于x的方程x2-3x+a=0和x2-3x+b=0(a≠b)的四个根组成首项为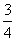 的等差数列,求a+b的值.
的等差数列,求a+b的值.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com