(四)初步运用，提高能力

1．(见课后练习题1．)

已知：点O是△ABC的垂心，OP⊥平面ABC．

求证：PA⊥BC．

(学生先思考，教师作如下点拨)

(1)什么叫做三角形垂心？

(2)点O是△ABC的垂心可以得到什么结论？

(3)可以考虑使用三垂线定理证明：你能找出本题中，应用三垂线定理必须涉及到的几个重要元素？

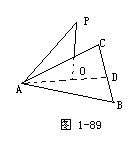
生：首先先确定一个平面--平面ABC，斜线是PA，PA在平面ABC上的射影是AD，∵AD垂直于BC，∴PA⊥BC．

师：他的回答是否有缺漏？

生：应该交代BC是平面ABC上的一条直线．

师：对，这个交代是必需的！(视学生程度作适当补充，用教具演示，还可以举反例说明．)

证明：连接AO并延长交BC与D．

师：三垂线定理是证明空间两条直线互相垂直的重要方法，上面的示例反映了应用三垂线定理解题的一般步骤，即确定一个平面、平面的垂线、斜线和斜线在平面上的射影．同时要注意的是平面内的一条直线和射影垂直，有这条直线和斜线垂直(定理)；平面内的一条直线和斜线垂直，有这条直线和射影垂直(逆定理)，同学们必须理解掌握．

2．(见课本例1)如果一个角所在平面外一点到角的两边距离相等，那么这一点在平面上的射影在这个角的平分线上．

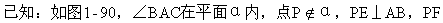
⊥AC，PO⊥α，垂足分别是E、F、O，PE＝PF．

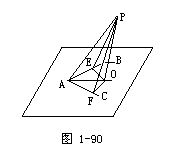
求证：∠BAO＝∠CAO．

(学生思考，教师作适当的点拨．)

(1)在平面几何中，证明点在角的平分线上的常规方法是什么？

(2)PE＝PF给我们提供了什么结论？

(3)所缺的垂直关系可以用三垂线定理或逆定理证明，你能列出证明所需的条件吗？

证明：

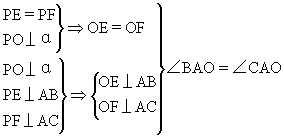
3．(课堂练习，师生共同完成．)

如图1-91，点P为平面ABC外一点，PA⊥BC，PC⊥AB，

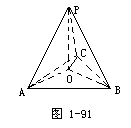
求证：PB⊥AC．

分析：证明直线与直线垂直的问题，可以考虑三垂线定理及其逆定理，图形中缺少的平面的垂线需要添加上去．

证明：过P作平面ABC的垂线，垂足为O，连结AO、BO、CO．

∵ PA⊥BC，∴AO⊥BC(三垂线逆定理)．

同理可证 CO⊥AB，∴O是△ABC的垂心．

∵OB⊥AC，∴PB⊥AC(三垂线定理)．

(三)层层推进，证明定理

师：猜测和实验的结论不一定正确，那么你想怎样证明这个猜想呢？

(若用幻灯或投影仪，可以节省板书时间．)

已知：PA、PO分别是平面α的垂线、斜线，AO是PO在平面α

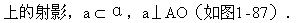
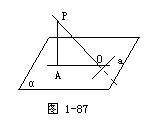
求证：a⊥PO．

师：这是证明两条直线互相垂直的问题，你准备怎么证明？

分析：从直线和平面垂直的定义可知，要证两条直线互相垂直，只要证明其中一条直线垂直于另一条直线所在的平面即可．

师：这个平面你找到了吗？

生：是平面PAO．

师：怎样证明a⊥平面PAO呢？

生：只要证明a垂直于平面PAO内的两条相交直线．

证明：

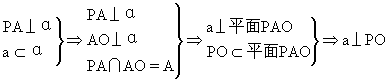
说明：

1．定理的证明，体现了“由线面垂直证明线线垂直”的方法；

2．上述命题反映了平面内的直线、平面的斜线和斜线在平面内的射影这三条直线之间的垂直关系，这就是著名的三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．

3．改变定理的题设和结论，得到逆命题：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直．可以用同样的方法证明，这就是三垂线定理的逆定理(请学生简要说明其证明方法和步骤)．

4．定理中包含了三个垂直关系：PA⊥α，AO⊥a，PO⊥a，

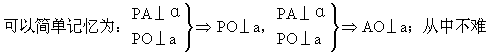
看出三垂线定理名称的来由．

5．从定理的条件看，关键的是直线和平面的相对位置关系，而与平面本身是否水平放置无关；在平面内的直线a与斜线或斜线的射影的位置关系关键在于垂直；这样直线a的如下四种位置关系，都是三垂线定理及其逆定理常见的情形．

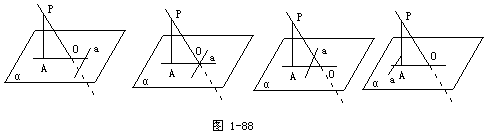
6．从定理的结论看，三垂线定理及其逆定理是判断直线垂直的重要命题．

(二)猜想推测，激发兴趣

师：根据直线与平面垂直的定义我们知道，平面内的任意一条直线都和平面的垂线垂直，那么，平面内的任意一条直线是否也都和平面的一条斜线垂直呢？

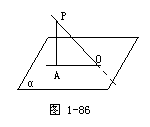
(教师演示教具，用一个三角板的一条直角边当平面的斜线，一根包有色纸的竹竿摆放在桌面的不同位置当作平面内的不同直线，学生容易看出它们不一定互相垂直．)

师：是否平面内的任意一条直线都不和这条平面的斜线垂直呢？

(教师将三角板的另一条直角边平放在桌面上，并提示学生注意这条直角边与平面的关系--在平面上，与斜线的关系--垂直．)

师：在平面上有几条直线和这条斜线垂直？

(学生可能会回答一条，也可能回答无数条，教师应调整桌面上的竹竿位置，使其平行于三角板的直角边，然后平行移动，并向学生说明，这些直线都与斜线垂直．)

师：平面内一条直线具备什么条件，才能和平面的一条斜线垂直？

(学生的直觉判断是要与那条和桌面接触的直角边平行，这是正确的，但无多大用途；这时教师提醒学生注意斜线在平面内的射影，并调整教具，将三角板的斜边当作平面的斜线，构成垂线、斜线和射影的立体模型；要求学生与同桌配合，摆放课前准备的竹签成教师示范的模型；然后在教师的引导之下观察、猜想，与同桌的探讨中发现了只要与斜线的射影垂直就和斜线垂直．)

三垂线定理及其逆定理的条件和结论都比较简单，但应用却很广泛，为了培养学生的能力，应让学生探索定理的命题形式，充分利用好手中的三根竹签．

设计学生活动符合建构主义的教学思想，也符合教师为主导、学生为主体的教学思想；教师根据教学要求，提出问题，创设情景，引导学生观察、猜想，主动发现，主动发展，从而调动了学生学习的积极性．

本课题共安排2课时，本节课为第一课时．

3．教学疑点及解决方法

(1)三垂线定理及其逆定理，揭示了平面内的直线与平面的垂线、斜线及斜线在平面内的射影这三条直线的垂直关系，其实质是平面内的一条直线与平面的一条斜线(或斜线在平面内的射影)垂直的判定定理．

(2)本节课的两个定理，涉及的直线较多，学生在认识和理解上都会存在困难，为了加深印象并说明复杂的直线位置关系，可以采用一些教具，或者让学生准备三根竹签，按照教师的要求摆放．在学生感性认识的基础上，进行理性的证明和记忆，有助于定理的掌握．

(3)三垂线定理是先有直线a垂直于射影AO的条件，然后得到a垂直于斜线PO的结论；而其逆定理则是已知直线a垂直于斜线PO，再推出a垂直于射影AO．在引用时容易引起混淆，解决的办法是，构造一个同时使用这两个定理的问题，引导学生分清．

(4)教学核心是定理的形成教学，教学的指导思想是：遵循由具体探究抽象、由简单到复杂的认识规律，启发学生反复思考，不断内化成为自己的认知结构．

2．教学难点：两个定理的证明及应用．

1．教学重点

(1) 掌握三垂线定理：在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直．

(2)掌握三垂线定理的逆定理：在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它也和这条斜线的射影垂直．

(三)德育渗透点

通过定理的论证和练习的训练渗透化繁为简的思想和转化的思想．