
|
题目 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
答案 |
D |
D |
A |
D |
B |
B |
A |
C |
B |
C |
《教学与测试》
3. 设 且
且 1° 求证
1° 求证 
2°比较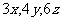 的大小。
的大小。
1° 证明:设 ∵
∵ ∴
∴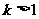
取对数得: 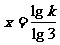


∴
2° 
∴
又:
∴ ∴
∴
2.(30课备用题1)已知
求证:
证明:由换底公式  由等比定理得:
由等比定理得:

 ∴
∴
∴
1.(29课备用题)证明:
证明: 设  ,
,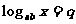 ,
,
则: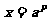


∴ 从而
从而 
∵  ∴
∴ 即:
即: (获证)
(获证)
注意:第30课 例一 1 及 例二 已于第二十二教时用过(可视情况处理)
3.对数的换底公式,及其推论。
2.对数的运算法则
作为一般要求,完成习题四11、12、13.
提高要求,完成以下两个补充练习:
1.如图1-92,PA⊥△ABC所在平面,AB=AC=13,BC=10,PA=5,求点P到直线BC的距离.
(五)归纳小结,强化思想
师:这节课,我们学习了三垂线定理及其逆定理,定理的证明方法是证明空间两条直线互相垂直的基本方法,我们称之为线面垂直法;还通过三个练习的训练加深了定理的理解,同时得到立体几何问题解决的一般思路.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com