解：∵ log₈ 3 = p　　　　　 ∴

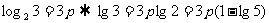
　　　　　　　　　　　 又∵ 　　　　∴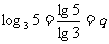 　

　　　　　　　　　　　 ∴ 　　　　　∴

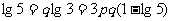
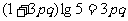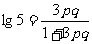
　　　　　 以下例题备用：

　　　　　　　　 证：∵　　　　 ∴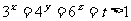

　　　　　　　　　　　　 ∴

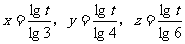
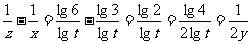
　　　　　　 解：∵ log ₁₈ 9 = a　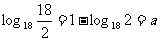　 ∴　　 ∴log₁₈ 2 = 1 - a

　　　　　　　　　　 ∵ 18 ^b = 5　　　　 ∴ log ₁₈ 5 = b　

　　　　　　　　　　 ∴　 　

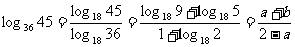
　　　　　　 解：1° 原式 =

　　　　　　　　　　 2° 原式 =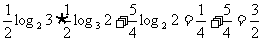

证：设 log _a N = x ,　 　则　 a ^x = N

　　　　 两边取以　 m 　为底的对数：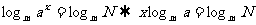

　　　　 从而得：　　　　 ∴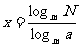

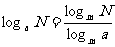
两个较为常用的推论：

1° 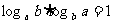　　　　　　　　　　2° 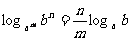( a, b > 0且均不为1)

证：1°

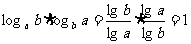
　　　　 2°

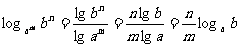
导入新课：对数的运算的前提条件是“同底”，如果底不同怎么办？

2．已知PA，PB，PC与平面α所成的角分别为60°，45°，30°，PO⊥平面α，O为垂足，又斜足A，B，C三点在同一直线上，且AB＝BC＝10cm，求PO的长．

作为一般要求，完成习题四9、10．

补充：

1．AB是直角三角形ABC的斜边，三个顶点在平面M的同侧，它们在M内的射影分别是A1、B1、C1，如果三角形A1B1C1是正三角形，且AA1＝3cm，BB1＝5cm，CC1＝4cm．求三角形A1B1C1的面积．

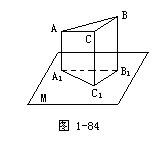
解：设正三角形A1B1C1的边长为x．

则AC2＝x2+1

BC2＝x2+1

AB2＝x2+22

∵AC2+BC2=AB2，

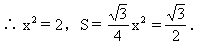
(四)例题分析

1．如图1-82，在正方体ABCD-A1B1C1D1中，E、F分别是AA1、A1D1的中点，求：

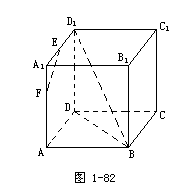
(1)D1B1与面AC所成角的余弦值；

(2)EF与面A1C1所成的角；

(3)EF与面AC所成的角．

解：

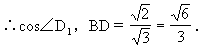
(2)45°．

(3)45°．

2．如图1-83，Rt△ABC的斜边AB在平面M内，AC和BC与M所成的角分别是30°、45°，CD是斜边AB上的高，求CD与M所成的角．

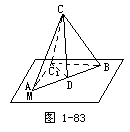
分析：作出CD与平面M所成的角，然后去解含这个角的三角形．

解：作CC1⊥平面M，连结AC1、BC1、DC1，依题意

∠CAC1＝30°，∠CBC1＝45°，设CC1＝a，则AC＝2a，

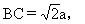
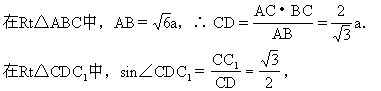
∴∠CDC1＝60°．

3．可让学生完成课后练习1、2．