1．外地人对衡阳人有哪些看法？有哪些典型言论？

6.文章最精彩的段落在哪里？为什么？

　通过点拨引导学生把握范文的特点：这篇杂文构思独特，它尽管是以记叙为主，对话贯穿全文，却包含着驳论文的本质特点，可以说是一个驳论过程的速写，给我们学写驳论文提供了一个很好的范例。狗摆事实，说道理，支撑起“人比狗更势利”的观点，这与人对狗的指责“你这势利的狗”针锋相对，从而有力地反驳人的“叱咤”，替自己正了名。文中最精彩的段落是列举人势利的论据段，人之所以由“傲慢”“叱咤”到“逃走”，就是被狗击中了要害。学生心领神会，深深地为鲁迅先生语言之精湛、思想之深刻所折服。

　最后，我引导学生：不能成为一棵凝聚着思想精华的参天大树，也要做一根会思想的芦苇。《狗的驳诘》批驳了人的势利，那么人性中还有哪些劣根、哪些陋习值得批驳呢？谁来驳诘最合理呢？它该怎样反驳呢？要求学生以《＿＿＿＿＿＿的驳诘》为题仿写。学生有茅塞顿开之感，思维非常活跃，不到20分钟，一篇篇意趣盎然的文章展现在眼前。让我们通过学生的命题来看看他们巧妙的构思吧：“猫的驳诘”“鼠的驳诘”“狼的驳诘”“花的驳诘”“狐狸的驳诘”“蟑螂的驳诘”“蝴蝶的驳诘”“黄鼠狼的驳诘”……更不乏生动幽默、思想深刻、见解新颖的精彩片段。如：

　蝴蝶的驳诘：“美丽招谁惹谁了？我没有涂脂抹粉，没有奢望霓裳羽衣，没有故作姿态，甚至没有想到过要利用美丽去达到什么目的，我美丽，我快乐，有什么错吗？”

　猫的驳诘：“时代在发展，鼠类的生存空间越来越小，为了赢得种族的生存，鼠辈们也越来越狡猾了，这都给我们的工作增加了难度。你们怎么能说我玩忽职守，犯有渎职罪呢？我没有收取‘硕鼠’贿赂的和氏璧而同意他承包检察院机关的整体搬迁工程；我也没有因为‘米老鼠’私下写信向上级部门举报我，就将‘莫须有’的罪名强加给她，判她十八年有期徒刑，或直接派人将她来个‘杀人灭口’；我甚至没有进过‘松鼠’开在森林里的‘迷你火锅城’，更别说去‘田鼠’的‘勿忘我娱乐总会’溜达溜达了……”

　鲁迅先生说：“‘会模仿’决不是劣点，我们正应该学习这‘会模仿’的，‘会模仿’又加以有创造，不是更好么？”(鲁迅《从孩子的照相说起》)这一课时，我指导训练的重点是引导学生从品味-感悟-模仿中，把握驳论文“击中要害”的艺术，激发学生的创新思维。

　课型二：引发学生的动情点，引导他们为情而写，为理而驳。

　这些年，作文教学的教坛上热热闹闹，风起云涌，“新概念作文”“创新作文”“想象作文”“反作文”等作文教学理念，使人眼花缭乱。其实洗尽铅华，返璞归真，作文开花结果的土壤乃生活，作文的本色是作者把自己对生活的思考艺术地表达出来，作文的生命缘于一个情字。驳论文的写作同样如此。规范的驳论文的写作对初三学生来说有点勉为其难，他们往往无从下手。因此我引导学生从生活中学写驳论文，引发其动情点，引导他们为情而写，为理而驳，观察生活，思考生活，在思考中自然而然地掌握反驳的技巧，同时又激发了学生对家乡的热爱，岂不是“一石三鸟”吗？

　这一节课，我首先在黑板上最醒目的位置板书了“丑陋的衡阳人”五个大字，绝大部分身为衡阳人的学生先是发笑，继而“不平”。这正是我要引导学生进入的情境，我还是以鲁迅先生为例引导学生。鲁迅弃医从文的动机就是缘于“我以我血荐轩辕”的赤子之情，他要医治国民麻木的灵魂，他要唤醒铁屋子里沉睡的人，于是他不仅仅是用笔，而更像是用一把解剖刀在剖析当时那个病态的社会，无情地揭露国民的劣根性，这正是因为“爱之深，恨之切”啊。因此，这堂课我们不仅仅是在学写作文，更是在反思。谁没有缺点呢？谁不值得反思呢？何况衡阳人本身就存在很多丑陋的地方，外地人对衡阳人也存在着很多偏见。从“有则改之，无则加勉”的角度看，写好今天这篇作文更是每个衡阳学子的神圣职责，也许你对衡阳人的某些病态的解剖可以引起患者和疗治专家的注意，那你或许就成了衡阳的功臣；同时针对外地人对衡阳人的某些偏见，作为一个衡阳人，我们更有责任反驳，以正视听。学生群情激奋，跃跃欲试。

　紧接着我引导学生就下列问题展开讨论：

5.狗正面立论的观点是什么？它是怎样支撑起自己的观点的？

4.狗要驳斥的对象是谁？它要反驳的观点是什么？它是怎样反驳的？

3.文中的狗对人首先是什么态度？然后又是什么态度？为什么会这样？

2.此文的主旨是什么？

1.此文的表达方式有什么特点？

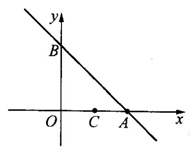
25．已知：如图，函数y=-x+2的图象与x轴、y轴分别交于点A、B，一直线L经过点C(1，0)将△AOB的面积分成相等的两部分．

　　 (1)求直线L的函数解析式；

　　 (2)若直线L将△AOB的面积分成1：3两部分，求直线L的函数解析式．

24．某产品每件成本10元，试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表：

　　 若日销售量y是销售价x的一次函数．

　　 (1)求出日销售量y(件)与销售价x(元)的函数关系式．

　　 (2)要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？

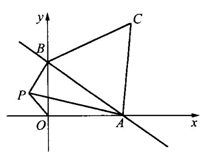
23．如图，一次函数y=-x+1的图象与x轴、y轴分别交于点A、B，以线段AB为边在第一象限内作等边△ABC．

　　 (1)求△ABC的面积．

(2)如果在第二象限内有一点P(a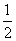，)，请用含a的式子表示四边形ABPO的面积，并求出当△ABP的面积与△ABC的面积相等时a的值．