
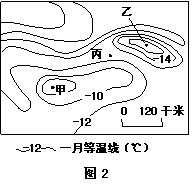
4、甲、乙、丙三地一月均温比较
A.甲地最高 B.乙地高于丙地
C.丙地高于甲地 D.乙地最高
下图中MN为北半球冬半年某日某一时刻地
球上完整的晨线。B点是MN线段的中点,M点的纬度数是68°,A点该日于北京时间8:40日出,18:00日落。读图回答5-- -7题。
-7题。

3、导致甲、乙两地1月等温线闭合的主要因素是
 A.纬度位置 B.距海远近
A.纬度位置 B.距海远近
C.大气环流 D.地形因素
2、该处自然保护区及水利枢纽分别是
A.卧龙 葛洲坝 B.神龙架 三峡
C.梵净山 葛洲坝 D.武夷山 三峡
图2是我国某地一月均温的等值线图,读图回答3---4题。
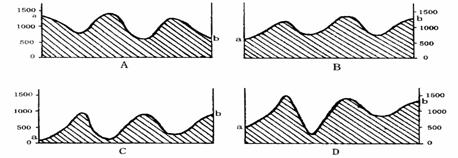
1、能正确反映图中沿a-b线所做的地形剖面图的是
1、已知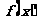 是二次函数,不等式
是二次函数,不等式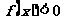 的解集是
的解集是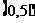 ,且
,且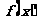 在区间
在区间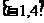 上的最大值
上的最大值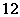 .
.
(1)求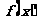 的解析式;
的解析式;
(2)是否存在自然数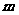 ,使得方程
,使得方程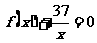 在区间
在区间 内有且只有两个不等的实数根?若存在,求出所有
内有且只有两个不等的实数根?若存在,求出所有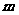 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(1)
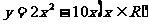
(2)假设满足要求的实数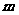 存在,则
存在,则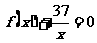 ,即有:
,即有: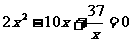
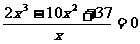 ,即有:
,即有: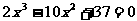
构造函数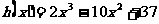
画图分析:
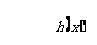

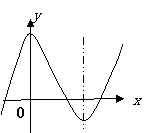
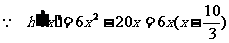
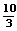
进而检验,知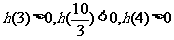 ,所以存在实数
,所以存在实数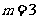 使得
使得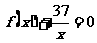 在区间
在区间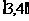 内有且只有两个不等的实数根。
内有且只有两个不等的实数根。
点评:本题关键是构造了函数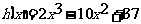 ,舍弃了原函数中分母
,舍弃了原函数中分母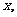 问题得到了简化。
问题得到了简化。
变式练习:设函数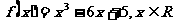 ,求已知当
,求已知当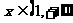 时,
时,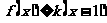 恒成立,求实数
恒成立,求实数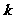 的取值范围。
的取值范围。
(2)抓住常规基本函数,利用函数草图分析问题:
例: 已知函数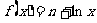 的图像在点
的图像在点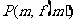 处的切线方程为
处的切线方程为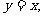
设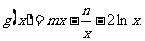
(1)
求证:当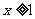 时,
时,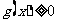 恒成立;
恒成立;
(2)
试讨论关于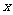 的方程
的方程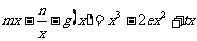 根的个数。
根的个数。
解证:(1)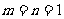
(2)方程 从而
从而 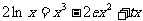
因为 所以方程可变为
所以方程可变为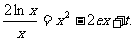
令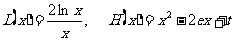 ,得:
,得: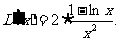
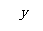
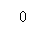
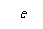
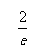
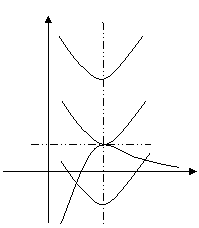 当
当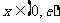 时,
时,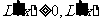 在
在 上为增函数;
上为增函数;
当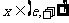 时,
时,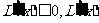 在
在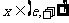 上为减函数;
上为减函数;
当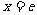 时,
时,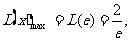
又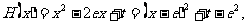
所以函数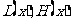 在同一坐标系的大致图像如图所示
在同一坐标系的大致图像如图所示
① 当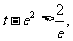 即
即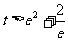 时,方程无解;
时,方程无解;
② 当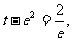 即
即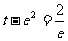 时,方程一解;
时,方程一解;
③ 当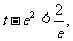 即
即 时,方程有2个根。
时,方程有2个根。
分析点评:一次函数,二次函数,指对数函数,幂函数,简单的分式根式函数,绝对值函数的图象力求清晰准确,一些综合性的问题基本上是这些函数的组合体,如果适当分解和调配就一定能找到问题解决的突破口,使问题简单化明确化。
(3)复合函数问题一定要坚持定义域优先的原则,抓住函数的复合过程能够逐层分解。
例:已知函数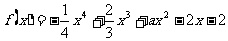 在区间
在区间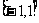 上单调递减,在区间
上单调递减,在区间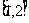 上单调递增。
上单调递增。
(1)
求实数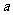 的值.
的值.
(2)
若关于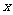 的方程
的方程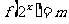 有3个不同的实数解,求实数
有3个不同的实数解,求实数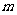 的取值范围.
的取值范围.
(3)
若函数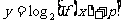 的图像与坐标轴无交点,求实数
的图像与坐标轴无交点,求实数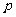 的取值范围。
的取值范围。
解:(1)利用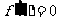 得:
得: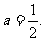
(2)因为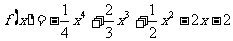
得  列表得
列表得

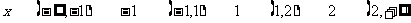





因此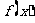 有极大值
有极大值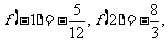 极小值
极小值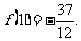 作出
作出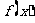 的示意图,
的示意图,
 如图:
如图:
因为关于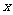 的方程
的方程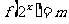 有3个不同
有3个不同
的实数解,令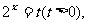 即关于
即关于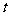 的方程
的方程
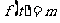 在
在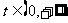 上有3个不同的实数解,
上有3个不同的实数解,
所以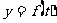 的图像与直线
的图像与直线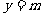 在
在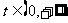
上有3个不同的交点。
而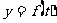 的图像与
的图像与 的图像一致。即
的图像一致。即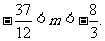
(3)函数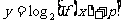 的图像与坐标轴无交点,可以分以下2种情况:
的图像与坐标轴无交点,可以分以下2种情况:
①当函数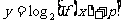 的图像与
的图像与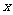 轴无交点时,则必须有
轴无交点时,则必须有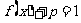 无解,而
无解,而
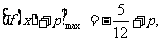 函数
函数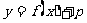 的值域为
的值域为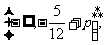 所以
所以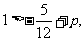
解得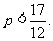
②当函数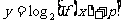 的图像与
的图像与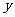 轴无交点时,则必须有
轴无交点时,则必须有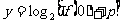 不存在,即
不存在,即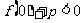 或
或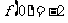 ,有意义,所以
,有意义,所以 ,解得
,解得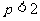 .
.
③由函数存在,可知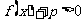 有解,解得
有解,解得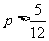 ,故实数
,故实数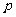 的取值范围为
的取值范围为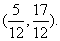
分析点评:复合函数尤其是两次复合,一定要好好掌握,构造两种函数逐层分解研究,化繁为简,导数仍然是主要工具。
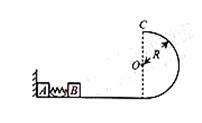
18. 光滑水平面上放着质量mA=1kg的物块A与质量mB=2kg的物块B,A与B均可视为质点,A靠在竖直墙壁上,A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接),用手挡住B不动,此时弹簧弹性势能Ep=49J.在A、B间系一轻质细绳,细绳长度大于弹簧的自然长度,如图所示,放手后B向右运动,绳在短暂时间内被拉断,之后B冲上与水平面相切的竖直半圆光滑轨道,其半径R=0.5m,B恰能到达最高点C。取g=10m/s2,求:
(1)B到达圆轨道底端时的速度大小。(4分)
(2)弹簧恢复原长的过程中弹力对B的冲量。(4分)
 (3)绳拉断后瞬间A的速度的大小。(4分)
(3)绳拉断后瞬间A的速度的大小。(4分)
17. 一辆汽车质量为m,从静止开始以恒定功率起动,沿水平方向前进了距离s,达到最大行驶速度vm。汽车所受阻力为车重的k倍,求:
(1)汽车的功率P(4分)
(2)汽车从静止到开始做匀速运动所需的时间。(4分)
(3)当速度为0.5Vm时汽车的加速度。(4分)
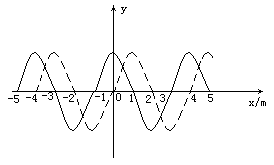
16.右图是一列简谐波在某一时刻的波形图线。虚线是0.2s后它的波形图线。求:
(1)波长是多少?(2分)
(2)若波向右传播,传播速度是多大?(4分)
(3)若传播速度为215m/s,波向哪个方向传播?(4分)
15.质量为1kg的小球,从高为5m处自由下落,跟地面碰撞后反弹的高度是3.2m,设碰撞时间为0.05s。求:(g取10m/s2)
(1)小球落地时速度的大小V1(2分)
(2)小球离开地面的速度大小V2。(2分)
(3)地板对小球的平均作用力。(4分)
14.把质量是1kg的石块从高为5m的平台上水平抛出,抛出的初速度为5m/s。求:
(1)抛出时人对石块做的功(2分)。
(2)石块即将落地时速度的大小(2分)。
(3)石块即将落地时重力做功的功率(2分)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com