4、用一块手帕浸泡在盛有质量分数为70%的酒精溶液中，浸透后取出，将手帕展开，用镊子夹住两角，用火柴点燃，当手帕上的火焰熄灭后，手帕安好无损，对于这一现象，下面的解释正确的是(　　 )

A、这是魔术，你看到的是一种假B、火焰的温度低于棉布的着火点

C、手帕上的水汽化吸热，使手帕的温度低于面部的着火点

D、酒精燃烧后使面部的着火点升高

3、下列说法正确的是　　　　　　　　　　　　　　　　 (　　 )

A、有发光、发热现象的变化一定是燃烧

B、剧烈的燃烧都会引起爆炸

C、爆炸一定是化学变化　 D、燃烧一定伴随着发光、放热的现象

2、小红在纸叠的小船中加入适量的水，用酒精灯直接加热，纸船安然无恙。纸船没有燃烧的主要原因　　　　　　　　　　　 (　　 )

A、纸不是可燃物　　　　　　　 B、没有和氧气接触

C、没有达到着火点　　　　　　 D、水能灭火

1、1992年海湾战争期间，科威特特大油井被炸起火燃烧，我国救援人员在灭火工作中做出了贡献，下列措施不能用于油井灭火的是(

)

A、设法降低石油的着火点　　　　 B、设法使火焰隔绝空气

C、设法阻止原油喷射　　　　　　 D、设法降低油井井口的温度

2．了解推论1的证明过程。

教学重点和难点

重点、难点：公理3的引入与掌握及推论1的证明。

教学过程

演示：用一根小棍作为直线的模型，一矩形硬纸板作为平面的模型，让学生自己也拿同样的模型，一起观察，再提出问题。

提问：(1)直线与平面有几种位置关系？

(2)直线和平面相交时，直线与平面有几个公共点？

(3)当直线与平面有几个公共点时，我们就能判定直线在平面内？

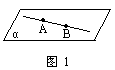公理1 　如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．(如图1)

这时我们说直线在平面内，或者说平面经过直线．

点A在直线a上，记作A∈a；

点A在直线a外，记作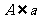

点A在平面α内，记作A∈α；

点A在平面α外，记作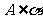

直线a在平面α内，记作

直线a在平面α外，记作

所以公理1用集合符号为：A∈a，B∈a，A∈α，B∈α，则

演示：：教师用矩形硬纸板的一顶点放在讲台面上，让学生观察，并同时提出问题．

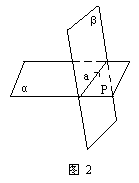问：看模型，能否说这两个平面只有一个公共点？

公理2 　如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线．(如图2)

公理2可记作：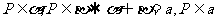

一扇门用两个合页和一把锁就可以固定了，但要注意，锁与合页不能放在同一直线位置上，否则，门也无法固定

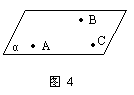公理3 　经过不在同一条直线上的三个点，有且只有一个平面．(如图4)

推论1 　经过一条直线和这条直线外一点，有且只有一个平面．

已知：点A，直线a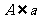，．(如图5)

求证：过点A和直线a可以确定一个平面．

证明：存在性．

因为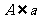，在a上任取两点B，C．

所以过不共线的三点A，B，C有一个平面α．(公理3)

因为B∈α，C∈α，

所以a∈α．(公理1)

故经过点A和直线a有一个平面α．

唯一性：如果经过点A和直线a的平面还有一个平面β，那么A∈β，a 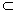β，

因为B∈a， C∈a，

所以B∈β，C∈β．(公理1)

故不共线的三点A，B，C既在平面α内又在平面β内．

所以平面α和平面β重合．(公理3)

所以经过点A和直线a有且只有一个平面．有时“有且只有一个平面”，我们也说“确定一个平面”．

类似地可以得出下面两个推论：

推论2 　经过两条相交直线，有且只有一个平面．(如图6)

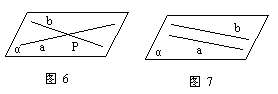推论3 　经过两条平行直线，有且只有一个平面．(如图7)

下面应用平面的基本性质证明空间有关点和直线的共面问题．(空间的几个点和几条直线，如果都在同一平面内，简单地说它们“共面”，否则说它们“不共面”)

例1 　两两相交且不过同一点的三条直线必在同一个平面内．(如图8)

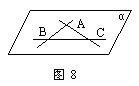已知：AB∩AC=A，AB∩BC=B，AC∩BC=C．

求证：直线AB，BC，AC共面．

证法一：因为AB∩AB=A，

所以直线AB，AC确定一个平面α．(推论2)

因为B∈AB，C∈AC，

所以B∈α，C∈α，

故BC 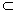α．(公理1)

因此直线AB，BC，CA都在平面α内，即它们共面．

证法二：

因为A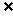直线BC上，

所以过点A和直线BC确定平面α．(推论1)

因为A∈α， B∈BC，所以B∈α．

故AB 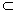α，

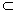同理AC α，

所以AB，AC，BC共面．

证法三：

因为A，B，C三点不在一条直线上，

所以过A，B，C三点可以确定平面α．(公理3)

因为A∈α，B∈α，所以AB 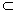α．(公理1)

同理B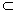C α，AC 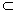α，所以AB，BC，CA三直线共面．

问题：(1)在这题中“且不过同一点”这几个字能不能省略，为什么？

作业

　　 课后练习

1．了解三个公理及公理3的三个推论；

23．(12分)质量为m=5kg的物体，置于倾角为a=37⁰的的固定斜面上，刚好匀速下滑。现对物体施加水平向右的推力F，使物体沿斜面匀速上升，设物体受到的最大静摩擦力等于滑动摩擦力(已知 g=10N/kg sin37⁰=0．6　　 cos37⁰=0．8)

(1)要求作出必要的受力图

(2)求物体与斜面间的动摩擦因素μ

(3)求推力F的大小。　　　

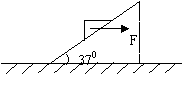
班级　　 　　　　　　　姓名　　　　　 　　　　　　　　　考号　　　　　

22．(12分)如图，位于水平地面上的重力为G的小木块，在大小为F、方向与水平方向成α角的拉力作用下沿地面向右作匀速直线运动。

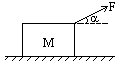(1)作出物体受力示意图,并合成或分解

　(2)求地面对物体的支持力FN

(3)求木块与地面之间的动摩擦因数μ

21．(12分)如图，接触面均光滑，球处于静止，球的重力为G=50N，斜面与水平面的夹角为30⁰

(1)作出物体受力示意图,并合成或分解

(2)求斜面对球的支持力

(3)求竖直挡板对球的弹力

20、轻弹簧秤上端固定于O点，下端悬挂-个光滑的定滑轮C，已知定滑轮C重力不计。木块A、B用跨过定滑轮的轻绳相连接，A、B的重力分别为5 N和2 N。整个系统处于平衡状态，如图所示，由图及物体状态可知，地面对木块A的支持力大小为________N，弹簧秤的示数是__________N。