
2.平行线与相交线:线段垂直平分线及性质;相交线中“两线四角”及“三线八角”中形成的对顶角、同位角、内错角、同旁内角等角与角之间的关系;平行线的性质及判定;平行线间的距离及平行线、垂线的画法等.
1.角:会计算角度;认识度、分、秒,会进行简单的换算;了解角平分线及其性质.
21.解:(Ⅰ)由题可得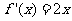 ................2分
................2分
所以曲线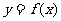 在点
在点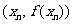 处的切线方程是:
处的切线方程是: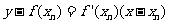 .
.
即 .
...............4分
.
...............4分
令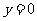 ,得
,得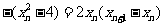 ,即
,即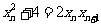 .
.
显然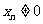 ,∴
,∴ .
..................6分
.
..................6分
(Ⅱ)由 ,知
,知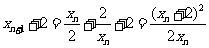 ,同理
,同理 .
.
故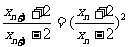 .
.
从而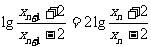 ,即
,即 .所以,数列
.所以,数列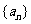 成等比数列. ...8分
成等比数列. ...8分
故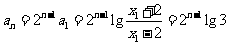 ,即
,即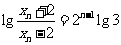 ,从而
,从而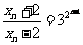 ,
,
所以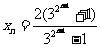 .
..................10分
.
..................10分
(Ⅲ)由(Ⅱ)知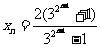 ,
,
∴ ;
...........12分
;
...........12分
∴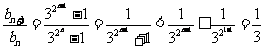 ,
,
故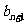 <
<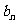 .
............14分
.
............14分
20.解:(1)由已知,点M到直线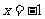 的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以
的距离等于到点(1,0)的距离,所以点M是以F(1, 0)为焦点,以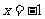 为准线的抛物线,焦点到准线的距离p = 2, ........2分
为准线的抛物线,焦点到准线的距离p = 2, ........2分
∴ 点M的轨迹方程为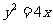 .
.........4分
.
.........4分
(2)设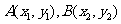 ,由
,由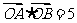 可得:
可得: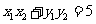 ①
①
∵ A、B均在抛物线上,
∴ 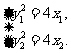 Þ
Þ 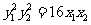 ②
②
由①②可得: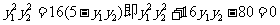 ,
,
∴ 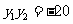 或
或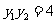 (舍去).
.............8分
(舍去).
.............8分
再由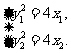 相减得:
相减得: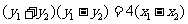 ,
,
若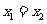 ,则AB⊥x轴,
,则AB⊥x轴,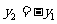 ,由①:
,由①: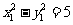 ,结合
,结合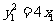 得:
得: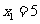 ,
,
∴ 此时AB的方程为 .
..............9分
.
..............9分
若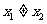 ,则
,则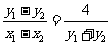 ,即为直线AB的斜率,而
,即为直线AB的斜率,而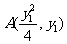 ,则AB的方程为:
,则AB的方程为:
 ,
.............11分
,
.............11分
即 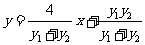 ,
,
∴ 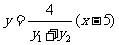 也过定点 (5, 0).
...............13分
也过定点 (5, 0).
...............13分
综上得,直线AB过定点 (5, 0). ...............14分
19.解:(1)证明:连结AC,AC交BD于O,连结EO
∵底面ABCD是正方形,∴点O是AC的中点
在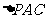 中,EO是中位线,∴PA // EO
中,EO是中位线,∴PA // EO
而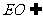 平面EDB且
平面EDB且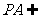 平面EDB,
平面EDB,
所以,PA // 平面EDB. ................4分
(2)证明:∵PD⊥底面ABCD且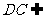 底面ABCD,∴
底面ABCD,∴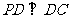
∵PD=DC,可知 是等腰直角三角形,而DE是斜边PC的中线,
是等腰直角三角形,而DE是斜边PC的中线,
 ∴
∴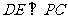
 ①
①
同样由PD⊥底面ABCD,得PD⊥BC
∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC
而 平面PDC,∴
平面PDC,∴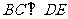
 ②
②
由①和②推得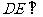 平面PBC
平面PBC
而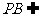 平面PBC,∴
平面PBC,∴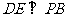
又 且
且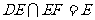 ,所以PB⊥平面EFD
,所以PB⊥平面EFD
.................8分
(3)∵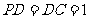 ,
,
由PD⊥平面ABCD,∴ PD⊥BC,
又∵ BC⊥CD,PD∩CD=D,∴BC⊥平面PCD,
∴ BC⊥PC.
在△BDE中,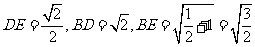 ,
,
∴ 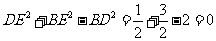 ,即DE⊥BE.
,即DE⊥BE.
而由(2),PB⊥平面EFD,有PB⊥DE,因而DE⊥平面BEF,
在Rt△BPD中, ,
,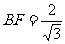 ;Rt△BEF中,
;Rt△BEF中,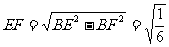 .
.
∴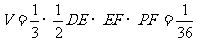 . ........14分
. ........14分
18.解: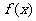 的定义域为
的定义域为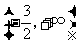 .
...............2分
.
...............2分
(Ⅰ)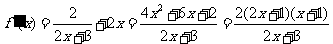 .............4分
.............4分
当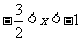 时,
时,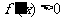 ;
;
当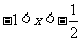 时,
时,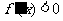 ;
;
当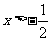 时,
时,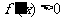 .
.................8分
.
.................8分
从而,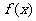 分别在区间
分别在区间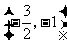 ,
,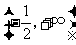 单调递增,在区间
单调递增,在区间 单调递减.
单调递减.
..................10分
(Ⅱ) 对任意
对任意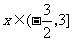 恒成立当且仅当在
恒成立当且仅当在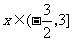 时,
时,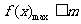 .
.
...............12分
由(Ⅰ)可知,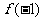 = 1是极大值,而
= 1是极大值,而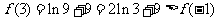 ,因而
,因而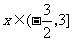 时,
时,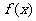 的最大值为2ln3 + 9,
的最大值为2ln3 + 9,
∴ m的取值范围是 [2ln3 + 9, +¥). ................14分
17.解:记“第i个人破译出密码”为事件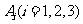 ,则
,则
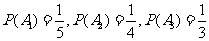 ...................2分
...................2分
(1)设“恰好二人破译出密码”为事件B,则有:
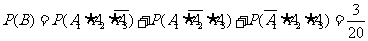 . ..........7分
. ..........7分
(2)设“密码被破译”为事件C,“密码未被破译”为事件D,则有:
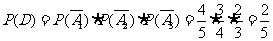 , .........10分
, .........10分
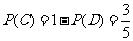 ,即密码被破译的概率为
,即密码被破译的概率为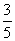 .
............12分
.
............12分
16.解:∵ 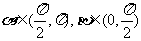 ,
,
∴ 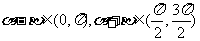 , ..................2分
, ..................2分
∴ 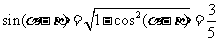 , ...................5分
, ...................5分
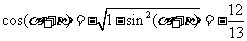 , ....................8分
, ....................8分
∴ 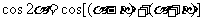
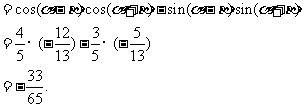
...................12分
(二)选做题(14-15题,考生只能从中选做一题)
14. .解析:因为
.解析:因为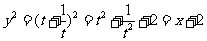 ,而
,而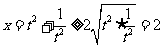 .
.
15.90°.解析:因为 是圆
是圆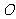 的切线,
的切线,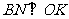 .有
.有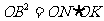 ,又
,又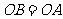 ,
,
所以 ,即
,即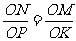 .又
.又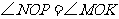 ,
,
所以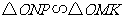 ,故
,故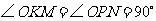 .
.
(一)必做题(11-13题)
11.2.解析:当x=-1时,即输出,此时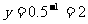 .
.
12.-18.解析: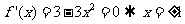 ,
,
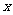 |
-3 |
(-3,-1) |
-1 |
(-1,1) |
1 |
(1,3) |
3 |
 |
|
- |
0 |
+ |
0 |
- |
|
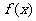 |
18 |
↘ |
-2 |
↗ |
2 |
↘ |
-18 |
故最小值为-18.
13.y2 = 4x.解析:由题意,则点P到直线x = -1的距离等于到点(1,0)的距离,则点P的轨迹是以(1,0)为焦点,以x = -1为准线的抛物线,即y2 = 4x.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com