
4.四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB,EF⊥AB,则EF与CD所成的角等于( )
A.30° B.45° C.60° D.90°
解析:取AD中点G,连结EG、GF,则GE 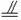
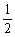 CD,GE=
CD,GE=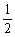 AB
AB
∵CD=2AB ∴GE=2GF,∵EF⊥AB,∴EF⊥GF.
∴∠GEF=30°
答案:A
3.在边长为a的正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=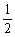 a,这时二面角B-AD-C的大小为( )
a,这时二面角B-AD-C的大小为( )
A.30° B.45° C.60° D.90°
解析:折起后△BCD为正三角形.
答案:C
2.平面α的斜线与α所成的角为30°,则此斜线和α内所有不过斜足的直线中所成的角的最大值为( )
A.30° B.60° C.90° D.150°
解析:本题易误选D,因斜线和α内所有不过斜足的直线为异面直线,故最大角为90°.
答案:C
1.异面直线a与b所成的角为50°,P为空间一点,则过P点且与a、b所成的角都是30°的直线有( )
A.1条 B.2条 C.3条 D.4条
解析:将a、b平移到点P,则过P与a、b所成的角都是30°的直线为2条.
答案:B
2.向量法是把求角的问题转化为求两向量的夹角.这里平面的法向量常用待定系数法求解,平面的法向量是关键.
学生练习
1.几何法一般要有三个步骤.
(1)作图:如上例中作出二面角的平面角及题中涉及的有关图形等;
(2)证明:证明所给图形是符合题设要求的;
(3)计算:在证明的基础上计算得出结果.
9.三种空间角的向量法计算公式:
⑴异面直线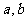 所成的角
所成的角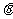 :
: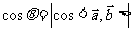 ;
;
⑵直线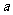 与平面
与平面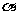 (法向量
(法向量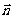 )所成的角
)所成的角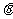 :
: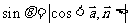 ;
;
⑶锐二面角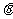 :
: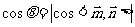 ,其中
,其中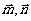 为两个面的法向量
为两个面的法向量
题型讲解
例1 直三棱柱A1B1C1-ABC,∠BCA=90°,点D1、F1分别是A1B1、A1C1的中点,BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
A.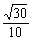 B.
B.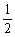 C.
C.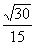 D.
D.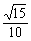
 解法一:(几何法)如图,连结D1F1,
解法一:(几何法)如图,连结D1F1,
则D1F1 
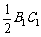
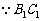
 BC ∴D1F1
BC ∴D1F1 
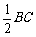
设点E为BC中点
∴D1F1  BE
BE 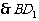
 EF1
EF1
∴∠EF1A或补角即为所求
由余弦定理可求得cos∠EF1A=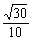 .
.
解法二:(向量法)建立如图所示的坐标系,设BC=1
则A(-1,0,0),F1(-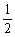 ,0,1),
,0,1),
B(0,-1,0),D1(-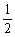 ,-
,-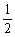 ,1)
,1)
即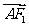 =(
=(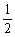 ,0,1),
,0,1),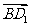 =(-
=(-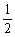 ,
,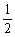 ,1)
,1)
∴cos<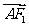 ,
,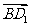 >=
>=
点评: 解法一与解法二从两个不同角度求异面直线所成的角.解法一体现传统方法作-证-算;解法二把角的求解转化为向量运算,应注意体会两种方法的特点.
例2 在正四面体ABCD中,E为AD的中点,求直线CE与平面BCD成的角.
分析:求线面角的关键在于找出斜线在平面内的射影,即找垂面,有了垂面即可在垂面内作交线的垂线,线面角即可作出,然后转化到三角形中求解.
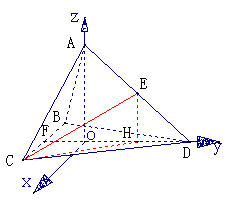 解法一: 取BC的中点F,连结AF、DF
解法一: 取BC的中点F,连结AF、DF
∵正四面体ABCD
∴BC⊥AF,BC⊥DF
∴BC⊥面AFD,
而BC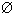 平面BCD
平面BCD
∴面AFD⊥面BCD
过E作EH⊥DF于H,
而DF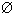 平面BCD,则EH⊥面BCD
平面BCD,则EH⊥面BCD
则∠ECH为CE与面BCD所成的角.
在Rt△CEH中,sin∠ECH= .
.
即CE与平面BCD成的角为arcsin .
.
解法二:如图建立以三角形BCD的中心O为原点,,OD,OA依次为y轴,z 轴X轴平行于BC
设正四面体ABCD的棱长为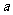 ,
,
则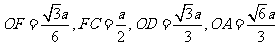
∴
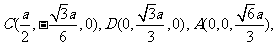
∵E为AD的中点,∴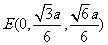
∴
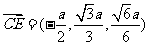
又因为平面BCD的法向量为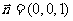 ,
,
∴即CE与平面BCD成的角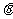 满足:
满足:
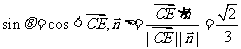
点评:求线面角的两种方法
例3 如图,在长方体ABCD-A1B1C1D1中,AB=2,BC=BB1=1,E为D1C1的中点,求二面角E-BD-C的正切值.
解法一:∵ABCD-A1B1C1D1是长方体,
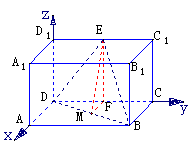 ∴作EF⊥面BCD,而E为
∴作EF⊥面BCD,而E为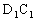 的中点,则F为CD的中点,过F作FM⊥BD交BD于M,连EM,由三垂线定理知EM⊥BD,
的中点,则F为CD的中点,过F作FM⊥BD交BD于M,连EM,由三垂线定理知EM⊥BD,
∴∠EMF就是二面角E-BD-C的平面角,)又∵AB=2,BB1=BC=1,EF=1,
FM=1×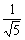 =
=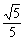
∴tan∠EMF=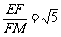 .
.
解法二:∵S△BDF=S△EBD·cosθ
而S△BDF=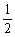 BD·FM=
BD·FM=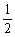 ·
·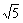 ·
·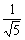 =
=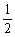 ,
,
又BD=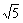 ,ED=
,ED=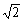 ,BE=
,BE=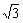
∴ED2+BE2=BD2
∴DE⊥EB 故S△EBD=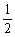 ED·EB=
ED·EB=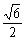
∴cosθ=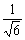 ;tanθ=
;tanθ=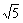 .
.
 解法三:过E作棱BD的垂线EM交BD于M,过C点作棱BD的垂线CN交BD于N,E、C是异面直线EM、CN上两点,CE=
解法三:过E作棱BD的垂线EM交BD于M,过C点作棱BD的垂线CN交BD于N,E、C是异面直线EM、CN上两点,CE=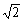 .EM=
.EM=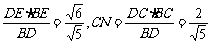 ,
,
而FM⊥BD,CN⊥BD,F为CD中点,
∴MN=DM=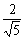
∴2=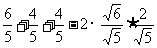 cosθ
cosθ
cosθ=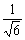 ,tanθ=
,tanθ=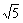 .
.
解法四:如图,建立坐标系,则D(0,0,0),B(1,2,0),E(0,1,1)
设平面DBE的方程为: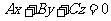 (过原点D=0)
(过原点D=0)
则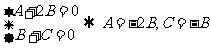
∴平面DBE的一个法向量为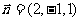
又因为平面BCD的一个法向量为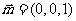
二面角E-BD-C的余弦值为:
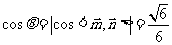
∴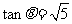
点评: 选此题意在通过此题使学生掌握二面角平面角的作法及求法.即三垂线定理及逆定理法,投影法,利用异面直线上两点间的距离公式法.
例4 正方体ABCD-EFGH的棱长为a,点P在AC上,Q在BG上,且AP=BQ=a,
⑴求直线PQ与平面ABCD所成的角的正切值;
⑵求直线PQ与AD所成的角
分析:(1)先作出PQ在面ABCD内的射影,由于面BFGC⊥面ABCD,作QM⊥BC于M,则MP就是QP在面ABCD内的射影,∠QPM就是要求的角,也可以先求出面ABCD的法向量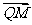 与
与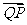 的角,然后再求它的余角即得
的角,然后再求它的余角即得
(2)(向量法)解:建立坐标系后,求出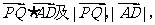
可由cos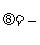
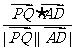 求解,
求解,
解(1)作QM⊥BC于M,连MP,则∠QMP就是直线PQ与平面ABCD所成的角则易得:QM=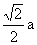 , MP=(1-
, MP=(1-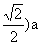
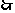 tan∠QPM=
tan∠QPM=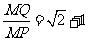
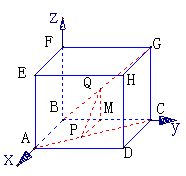 (2)建立空间直角坐标系如图,则
(2)建立空间直角坐标系如图,则
Q(0,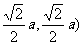 P(
P(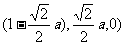
A(a,0,0),D(a,a,0),
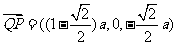 ,
,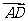 =(0,a,0)
=(0,a,0)
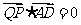
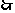 QP与AD所成的角为90°
QP与AD所成的角为90°
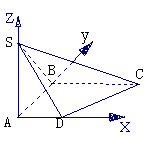 例5 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=
例5 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=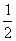 ,求面SCD与面SBA所成的二面角的正切值
,求面SCD与面SBA所成的二面角的正切值
分析:此题中二面角的棱没有画出,按常规解可延长BA,CD相交于E,则SE是二面角的棱,因为DA⊥面ABS,过点A作SE的垂线交SE于F,连结DF,则∠ADF就是所求二面角的平面角
若用向量法求解,就是要求两个面的法向量所成的角或补角
解:如图建立空间直角坐标系,则依题意可知D(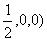 ,C(1,1,0),
,C(1,1,0),
S(0,0,1),可知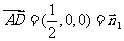 是面SAB的法向量
是面SAB的法向量
设平面SCD的法向量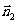 =(x,y,z)
=(x,y,z)

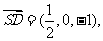
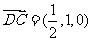
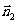
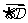 =0,
=0,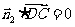
可推出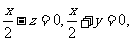 令x=2,则有y=-1,z=1,
令x=2,则有y=-1,z=1,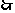
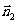 =(2,-1,1)
=(2,-1,1)
设所求二面角的大小为θ,则
cosθ=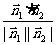 =
=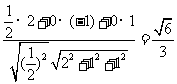
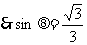 , tan
, tan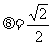
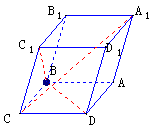
例6 已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD
(1)证明:C1C⊥BD;
(2)当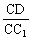 的值为多少时,能使A1C⊥平面C1BD请给出证明
的值为多少时,能使A1C⊥平面C1BD请给出证明
证明:如设∠C1CB=θ,由题设,∠C1CD=∠BCD=θ 令
令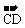 =
=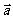 ,
,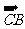 =
=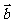 ,
, =
=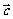 ,|
,|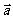 |=1,|
|=1,|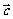 |=x,因为四边形ABCD为菱形,所以|
|=x,因为四边形ABCD为菱形,所以|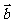 |=1,
|=1,
 (1)∵
(1)∵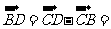
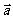 -
-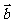
∴ 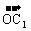 ·
·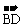 =
=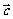 ·(
·(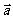 -
-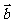 )=
)=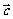 ·
·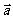 -
-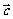 ·
·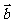
=1·x·cosθ-1·x·cosθ=0
∴ C1C⊥BD
(2)假设A1C⊥平面C1BD成立
则A1C⊥C1D,从而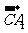 ·
·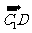 =0
=0
由于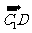 =
=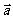 -
-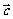 ,
,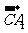 =
=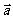 +
+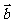 +
+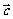
因此
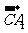 ·
·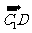 =(
=(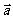 +
+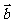 +
+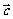 )·(
)·(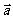 -
-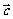 )
)
= 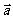 2+
2+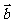 ·
·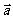 +
+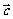 ·
·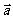 -
-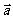 ·c-
·c-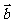 ·
·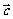 -
-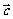 2
2
=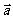 2+
2+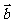 ·
·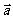 +
+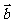 ·
·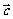 -
-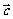 2=1+1·1·cosθ-1·x·cosθ-x2
2=1+1·1·cosθ-1·x·cosθ-x2
=(1-x)(1+x+cosθ)
从而(1-x)·(1+x+cosθ)=0
由于1+x+cosθ>0,因此,x=1
也就是说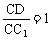 时,A1C⊥平面C1BD成立
时,A1C⊥平面C1BD成立
点评:平行六面体的12条棱共分三组,每组四条棱两两平行,故可取共顶点的三条棱作为空间向量的基底,此题中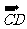 ,
,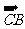 ,
, 三个共点向量为基底,其余向量可由此三个向量生成
三个共点向量为基底,其余向量可由此三个向量生成
小结:
空间角的求解有两种方法一种是几何法,另一种是向量法.
7.二面角的求法:⑴几何法;⑵向量法
8求二面角的射影公式: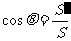 ,
,
其中各个符号的含义是: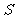 是二面角的一个面内图形F的面积,
是二面角的一个面内图形F的面积, 是图形F在二面角的另一个面内的射影,
是图形F在二面角的另一个面内的射影,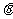 是二面角的大小
是二面角的大小
6.二面角的平面角:
(1)过二面角的棱上的一点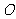 分别在两个半平面内作棱的两条垂线
分别在两个半平面内作棱的两条垂线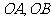 ,则
,则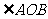 叫做二面角
叫做二面角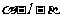 的平面角
的平面角
(2)一个平面垂直于二面角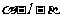 的棱
的棱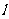 ,且与两半平面交线分别为
,且与两半平面交线分别为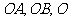 为垂足,则
为垂足,则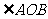 也是
也是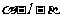 的平面角
的平面角
说明:①二面角的平面角范围是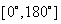 ;
;
②二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直
4.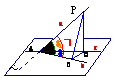 公式:平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有
公式:平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有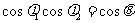
5二面角:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面若棱为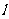 ,两个面分别为
,两个面分别为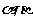 的二面角记为
的二面角记为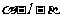 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com