作为一般要求，完成习题四1、2、3、4．

提高要求，完成以下两个补充练习：

1．如图1-70，在正方形ABCD中，E、F分别是BC、CD的中点，G是EF的中点，现在沿AE、AF及EF把这个正方形折成一个空间图形，使B、C、D三点重合，重合后的点记为H，那么，在这个空间图形中必有　　　　　　　　　　　　　　　　　　　　　　　　　　　 [　　 ]

A、AH⊥△EFH 所在平面

B、AD⊥△EFH所在平面

C、HF⊥△AEF所在平面

D、HD⊥△AEF所在平面

答案：选择(A)

∵AH⊥EH，AH⊥FH，

∴AH⊥平面EFH．

讲评作业时说明：应用折叠不变性设计的本题，目的是用于培养学生的空间想象能力和“转化”思想方法；折叠问题要注意应用折叠前、后平面图和立体图中，各个元素间大小和位置关系不变的量．

(四)初步运用，提高能力

例1　 如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面．

分析：首先写出已知条件和结论，并画图形．

已知：a∥b，a⊥α　 (如图1-68)．

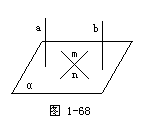
求证：b⊥α，

要证明：b⊥α，根据判定定理，只要证明在平面α内有两条相交直线m、n与b垂直即可．

证明：在平面α内作两条相交直线m、n，设m∩n＝A．

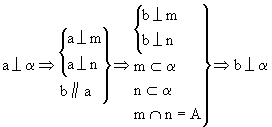
说明：

1．本例可以作为直线和平面垂直的又一个判定定理．这样，判定一条直线与已知平面垂直，可以用这条直线垂直于平面内两条相交直线来证明，也可以用这条直线的平行直线垂直于平面来证明．

2．课本书写的证明过程比较简洁，最好要求学生按照本教案示例书写．

练习(课后练习2)求证：如果三条共点直线两两垂直，那么其中一条直线垂直于另两条直线确定的平面．

已知：OA⊥OB，OB⊥OC，OC⊥OA．

求证：

OA⊥平面BOC，OB⊥平面AOC，OC⊥平面AOB．

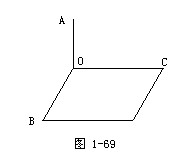
证明：(以证明OA⊥平面BOC为例，目的是强化书写格式)

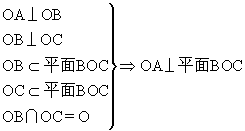
(三)层层推进，证明定理

指导学生写出已知条件和结论，并画出图形如右：

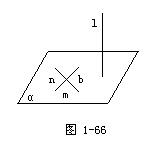
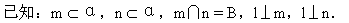
求证：l⊥α

师：你如何证明直线和平面垂直呢？

生：根据直线和平面垂直的概念，只需证明该直线和平面内的任何一条直线都垂直即可．

师：设g是平面α内的任意一条直线，现在只要证明l⊥α就可以了．对于平面α内不经过点B的直线，可以过点B作它的平行直线，所以，我们先证明l，g都经过点B的情况．

(生思考证明方法，教师在原有图形上适时添加辅助线，并对下列问题根据需要作提示．)

1．l、g是相交直线，要证它们垂直，实际上已经转化为平面几何中的垂直证明问题，可以考虑等腰三角形的性质．在直线l上点B的两侧分别取点A，A′，使AB＝A′B．

2．直线m、n和线段AA′是什么关系？

(m、n垂直平分AA′)

3．从结论看，直线g与线段AA′应当有什么关系？(g垂直平分AA′)

4．怎样证明直线g垂直平分线段AA′？

(只要g上一点E，有EA＝EA′)

5．过E作直线分别与m、n交于C、D，连结AC、A′C、AD、A′D，则有：AC＝A′C、AD＝A′D，由此能证明EA＝EA′吗？

(利用全等三角形性质)

(学生叙述证明过程，教师板书主要步骤．)

参看右图并作如下说明：

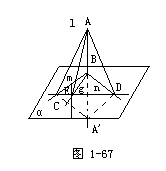
1．当直线g与m(或n)重合时，结论是显然的．

2．如果直线l、g有一条或两条不经过点B，那么可过点B引它们的平行直线，由过点B的这样两条直线所成的角，就是直线l与g所成的角，同理可证这两条直线垂直，因而l⊥g．

3．要判断一条已知直线和一个平面是否垂直，取决于在这个平面内能否找出两条相交直线和已知直线垂直，至于这两条相交直线是否和已知直线有公共点，是无关紧要的．

这样我们有了直线和平面垂直的判定定理．

(板书)如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面．

4．强调定理中“两条”和“相交直线”这两个条件的重要性，可举下面两个反例，加深学生的理解．

(1)将一块木制的大三角板的一条直角边AC放在讲台上演示，这时另一条直角边BC就和讲台上的一条直线(即三角板与桌面的交线AC)垂直，但它不一定和讲台桌面垂直．

(2)在讲台上放一根平行于大三角板直角边AC的木条EF，那么三角板的直角边BC也垂直于EF，但它不一定和讲台桌面垂直．

(二)猜想推测，激发兴趣

1．教师演示课本上的实例并指出书脊(想象成一条直线)、各书页与桌面的交线，由于书脊和书页底边(即与桌面接触的一边)垂直，得出书脊和桌面上所有直线垂直，书脊和桌面的位置关系给了我们以直线和平面垂直的形象．从而引入概念：一条直线和平面内的任何一条直线都垂直，我们说这条直线和这个平面互相垂直，直线叫做平面的垂线，平面叫做直线的垂面．

2．指出：过一点有且只有一条直线和一个平面垂直；过一点有且只有一个平面和一条直线垂直．平面的垂线和平面一定相交，交点叫做垂足．

3．说明直线和平面垂直的画法及表示．

师：要证明一条直线和一个平面垂直，若每次都要证明这条直线和平面上每一条直线都垂直，显然是很麻烦也不必要的．让我们先看看木工师傅是如何判断一根立柱是否和板面垂直的方法：用曲尺检查两次(只要两次，但曲尺靠板面的尺，两次不能在同一条直线上)，如果立柱、板面都和曲尺的两条边完全吻合，便可断定立柱和板面垂直．从中你能得到判定直线和平面垂直的方法吗？(引导学生进行猜想推测)

本课题共安排2课时，本节课为第一课时．

3．教学疑点：判定定理的条件中，“相交”是关键，“两条”也是一个重要条件，对于初学立体几何的学生来讲，是不好理解的，教师应该用实例说明这两个条件缺一不可．

2．教学难点：在于线、面垂直定义的理解和判定定理的证明；同时还要解决好定理证明过程中，辅助线添加的方法和原因，及为何可用经过B点的两条直线说明“任意”直线的问题．

1．教学重点

(1)掌握直线和平面垂直的定义：如果一条直线和一个平面内的任何一条直线垂直，那么这条直线就和这个平面垂直．

(2)掌握直线和平面垂直的判定定理：

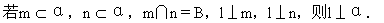
(3)掌握线线平行的性质定理：

若a∥b，a⊥α则b⊥α．