
20.(本小题满分12分)
 甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:
甲乙两人连续6年对某县农村鳗鱼养殖业的规模(总产量)进行调查,提供了两个方面的信息,分别得到甲、乙两图:

甲调查表明:每个鱼池平均产量直线上升,从第1年1万只鳗鱼上升到第6年2万只.
乙调查表明:全县鱼池总个数直线下降,由第1年30个减少到第6年10个.
请你根据提供的信息说明:
(Ⅰ)第2年全县鱼池的个数及全县出产的鳗鱼总数.
(Ⅱ)到第6年这个县的鳗鱼养殖业的规模比第1年扩大了还是缩小了?说明理由.
(Ⅲ)哪一年的规模(即总产量)最大?说明理由.
19.(本小题满分12分)
在平面直角坐标系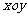 中,直线l与抛物线
中,直线l与抛物线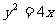 相交于不同的
相交于不同的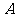 、
、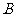 两点.
两点.
(Ⅰ)如果直线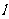 过抛物线的焦点,求
过抛物线的焦点,求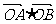 的值;
的值;
(Ⅱ)如果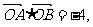 证明直线
证明直线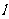 必过一定点,并求出该定点.
必过一定点,并求出该定点.
18.(本小题满分12分)
某种产品的广告费支出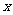 与销售额
与销售额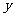 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
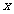 |
2 |
4 |
5 |
6 |
8 |
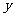 |
 30 30 |
40 |
60 |
50 |
70 |
(Ⅰ)画出散点图;
(Ⅱ)求回归直线方程;(参考数据: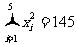
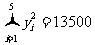
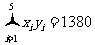 )
)
(Ⅲ)试预测广告费支出为10万元时,销售额多大?
17.(本小题满分12分)
已知命题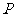 :“函数
:“函数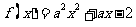 在
在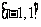 上存在零点”;
命题
上存在零点”;
命题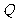 :“只有一个实数
:“只有一个实数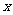 满足不等式
满足不等式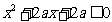 ”,若命题
”,若命题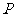 或
或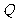 是假命题,求实数
是假命题,求实数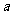 的取值范围.
的取值范围.
16.给出下列四个命题:
①命题“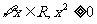 ”的否定是“
”的否定是“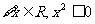 ”;
”;
②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强;
③抛物线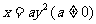 的焦点为
的焦点为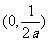 ;
;
④函数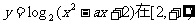 上恒为正,则实数a的取值范围是
上恒为正,则实数a的取值范围是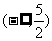 .
.
其中真命题的序号是 .(填上所有真命题的序号)
15.定义运算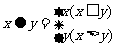 ,若
,若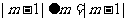 ,则
,则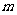 的取值范围是
的取值范围是
14.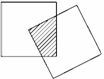 现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是
现有一个关于平面图形的命题:如图所示,同一个平面内有两个边长都是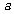 的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为
的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为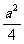 .类比到空间,有两个棱长均为
.类比到空间,有两个棱长均为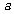 的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
13.设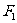 和
和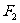 为双曲线
为双曲线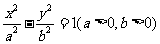 的两个焦点, 若
的两个焦点, 若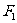 、
、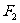 、
、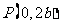 是正三角形的三个顶点,则双曲线的离心率为 .
是正三角形的三个顶点,则双曲线的离心率为 .
12.设椭圆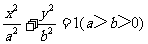 的离心率为
的离心率为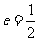 ,右焦点为
,右焦点为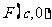 ,方程
,方程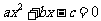 的两个实根分别为
的两个实根分别为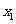 和
和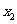 ,则点
,则点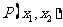
A.必在圆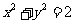 内
B.必在圆
内
B.必在圆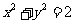 上
上
C.必在圆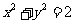 外
D.以上三种情形都有可能
外
D.以上三种情形都有可能
第Ⅱ卷(共90分)
11.函数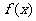 在定义域R内可导,若
在定义域R内可导,若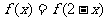 ,且当
,且当 时,
时,
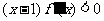 ,设
,设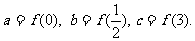 则
则
A.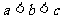 B.
B.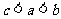 C.
C.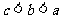 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com