7．If you are always _________ by such kind of failures, you will never succeed.

　　 A. turned down　　　　 B. cast down　　　　 C. made down　　　　　　　 D. put down

6．The genes of the cloned animals are so arranged that it can't________ such a disease, so it soon died.

　　　 A. overlook　　　　　　 B. resist　　　　　 C. exist　 D. withdraw

5．__________ news came _______ the H1N1Flu was spreading among children.

　　　 A. Disturbing; that　 　 B. Disturbed; which 　C. Disturbing; which　 D. Disturbed; what

4．_________ is no possibility __________ human being can be cloned in large numbers.

A.　　　　　 There; that　　　　　　　 B. It ; that　　　　　　　　　　 C. There; whether　　　　 D. It; whether

3．Only when the final examination is coming ___________ he had quite a lot to do.

　　　 A. he realized　　　　 B. he had realized　 C. did he realize　　　 D. had he realized

第一节：单项填空(共20小题；每小题0.5分，满分10分)

从A.B.C.D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项标号涂黑。1．－Shall I look after your house while you are away?

　 －______.

A.　 It couldn't be better.　 　 B. Of course you can.　　 C. If you like. D. It's up to you.

2．Every possible means _________ to prevent the spread of disease.

　　　 A. have tried　　　　　　　　 B. have been tried　　　　　　　　 C. has tried　　　　　　 D. has been tried

35、(2008年广州市数学中考试题)21、(12分)如图8，一次函数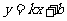的图象与反比例函数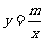的图象相交于A、B两点

(1)根据图象，分别写出A、B的坐标；

(2)求出两函数解析式；

(3)根据图象回答：当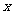为何值时，

一次函数的函数值大于反比例函数的函数值

36(2008年聊城市)(本题满分10分)已知一次函数与反比例函数的图象交于点．(1)求这两个函数的函数关系式；

(2)在给定的直角坐标系(如图)中，画出这两个函数的大致图象；

(3)当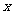为何值时，一次函数的值大于反比例函数的值？当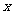为何值时，一次函数的值小于反比例函数的值？

33、2008年甘肃省白银市)如图是某种蜡烛在燃烧过程中高度与时间之间关系的图像，由图像解答下列问题：

(1)此蜡烛燃烧1小时后，高度为　　　　 cm；经过　　　　 小时燃烧完毕；

(2)求这个蜡烛在燃烧过程中高度与时间之间关系的解析式．

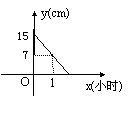
34(200(2008年湖北省宜昌市)8年湖北省宜昌市)为积极响应党中央关于支援5·12汶川地震灾区抗震救灾的号召，宜家工厂日夜连续加班，计划为灾区生产m顶帐篷.生产过程中的剩余生产任务y(顶)与已用生产时间x(时)之间的关系如图所示.

(1)求变量y与x之间的关系式.

(2)求m的值.

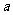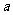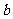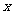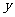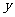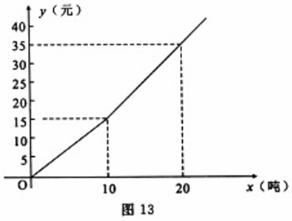
31、(2008襄樊市)我国是世界上严重缺水的国家之一．为了增强居民节水意识，某市自来水公司对居民用水采用以户为单位分段计费办法收费．即一月用水10吨以内(包括10吨)的用户，每吨收水费元；一月用水超过10吨的用户，10吨水仍按每吨元收费，超过10吨的部分，按每吨元()收费．设一户居民月用水吨，应收水费元，与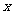之间的函数关系如图13所示．

(1)求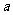的值；某户居民上月用水8吨，应收水费多少元？

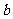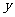(2)求的值，并写出当时，与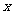之间的函数关系式；

(3)已知居民甲上月比居民乙多用水4吨，两家共收水费46元，求他们上月分别用水多少吨？

32(2008年广东湛江市)26． 某农户种植一种经济作物，总用水量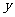(米)与种植时间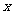(天)之间的函数关系式如图10所示．

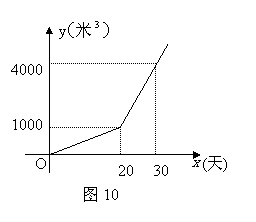(1)第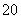天的总用水量为多少米？

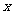
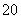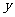(2)当时，求与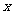之间的函数关系式．

(3)种植时间为多少天时，总用水量达到7000米？

2．(2008年湖北省咸宁市)如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．

实验与探究：

(1)　　 由图观察易知A(0，2)关于直线l的对称点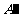的坐标为(2，0)，请在图中分别标明

B(5,3) 、C(-2,5) 关于直线l的对称点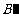、的位置，并写出他们的坐标:

　　　　　　 、　 　　　　　　；

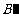归纳与发现：

(2)　　 结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点的坐标为　　　　　　 (不必证明)；

运用与拓广：

(3)　　 已知两点D(1,-3)、E(-1,-4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．

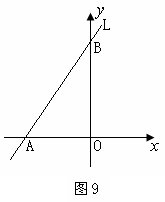
30(梅州)如图9所示，直线L与两坐标轴的交点坐标分别是A(-3，0)，B(0，4)，

O是坐标系原点．

(1)求直线L所对应的函数的表达式；

(2)若以O为圆心，半径为R的圆与直线L相切，求R的值．