
4、若关于x的不等式x2
+ bx + c < 0 的解为-2<x<-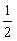 ,则不等式cx2-bx+1>0
,则不等式cx2-bx+1>0
的解为( )
(A)x<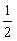 或x>2
(B)
或x>2
(B)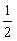 <x<2
<x<2
(C)-2<x<-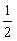 (D)x<-2或x>-
(D)x<-2或x>-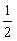
3、已知等差数列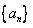 的前项和为
的前项和为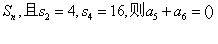
A.11 B.16 C.20 D.28
2、已知P:(x+3)2=0,Q:(x+3)2 +y2=0,其中x,y∈R,则P是Q成立的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充分条件 (D)既非充分也非必要条件
1、函数y=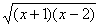 的定义域是( )
的定义域是( )
(A) {x|x≥1或x≤-2} (B){ x|-1≤x≤2}
(C) {x|x≥2或x≤-1} (D){ x|-2≤x≤1}
9.求异面直线所成的角的方法:
几何法:(1)通过平移,在一条直线上找一点,过该点做另一直线的平行线;(2)找出与一条直线平行且与另一条相交的直线,那么这两条相交直线所成的角即为所求
向量法:用向量的夹角公式
10两条异面直线的公垂线、距离
和两条异面直线都垂直相交的直线,我们称之为异面直线的公垂线
理解:因为两条异面直线互相垂直时,它们不一定相交,所以公垂线的定义要注意“相交”的含义.
两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线间的距离.
两条异面直线的公垂线有且只有一条
计算方法:①几何法;②向量法
题型讲解
 例1 A是△BCD平面外的一点,E、F分别是BC、AD的中点,
例1 A是△BCD平面外的一点,E、F分别是BC、AD的中点,
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角
(1)证明:用反证法
假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A、B、C、D在同一平面内,这与A是△BCD平面外的一点相矛盾故直线EF与BD是异面直线
(2)解:取CD的中点G,连结EG、FG,则EG∥BD,所以相交直线EF与EG所成的锐角或直角即为异面直线EF与BD所成的角在Rt△EGF中,求得∠FEG=45°,即异面直线EF与BD所成的角为45°
点评: ①证明两条直线是异面直线常用反证法;②求两条异面直线所成的角,首先要判断两条异面直线是否垂直,若垂直,则它们所成的角为90°;若不垂直,则利用平移法求角,一般的步骤是“作(找)-证-算”注意,异面直线所成角的范围是(0,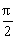 ]
]
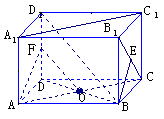
例2 长方体ABCD-A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:
(1)下列异面直线之间的距离:AB与CC1;AB与A1C1;AB与B1C
(2)异面直线D1B与AC所成角的余弦值
(1)解:BC为异面直线AB与CC1的公垂线段,
故AB与CC1的距离为b
AA1为异面直线AB与A1C1的公垂线段,故AB与A1C1的距离为c
过B作BE⊥B1C,垂足为E,则BE为异面直线AB与B1C的公垂线,BE=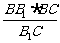 =
=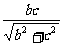 ,即AB与B1C的距离为
,即AB与B1C的距离为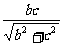
(2)解法一:连结BD交AC于点O,取DD1的中点F,连结OF、AF,则OF∥D1B,∴∠AOF就是异面直线D1B与AC所成的角
 ∵AO=
∵AO=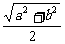 ,
,
OF= BD1=
BD1=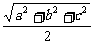 ,
,
AF=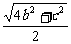 ,
,
∴在△AOF中,
cos∠AOF=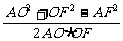 =
=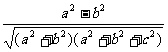
解法二:如下图,在原长方体的右侧补上一个同样的长方体,连结BG、D1G,则AC∥BG,∴∠D1BG(或其补角)为D1B与AC所成的角
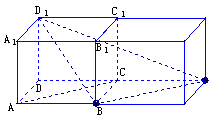 BD1=
BD1=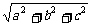 ,
,
BG=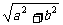 ,
,
D1G=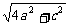 ,
,
在△D1BG中,
cos∠D1BG=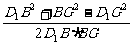 =-
=-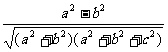 ,
,
故所求的余弦值为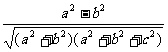
解法三:建立空间直角坐标系,写出坐标,用向量的夹角公式计算
例3 设异面直线a与b所成的角为50°,O为空间一定点,试讨论,过点O与a、b所成的角都是θ(0°≤θ≤90°)的直线l有且仅有几条?
解:过点O作a1∥a,b1∥b,则相交直线a1、b1确定一平面αa1与b1夹角为50°或130°,设直线OA与a1、b1均为θ角,作AB⊥面α于点B,BC⊥a1于点C,BD⊥b1于点D,记∠AOB=θ1,∠BOC=θ2(θ2=25°或65°),则有cosθ=cosθ1·cosθ2因为0°≤θ1≤90°,所以
0≤cosθ≤cosθ2
当θ2=25°时,由0≤cosθ≤cos25°,得25°≤θ≤90°;
当θ2=65°时,由0≤cosθ≤cos65°,得65°≤θ≤90°
故当θ<25°时,直线l不存在;当θ=25°时,直线l有且仅有1条;
当25°<θ<65°时,直线l有且仅有2条;
当θ=65°时,直线l有且仅有3条;
当65°<θ<90°时,直线l有且仅有4条;
当θ=90°时,直线l有且仅有1条
点评:异面直线所成的角就是选点、平移后的平面角上述解答首先将问题转化为:求过点O与a1、b1均成θ角的直线的条数,进而通过讨论θ的范围去确定直线l的条数
例4
如下图,设△ABC和△A1B1C1的三对对应顶点的连线AA1、BB1、CC1相交于一点O,且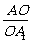 =
=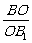 =
=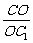 =
=
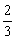 试求
试求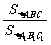 的值
的值
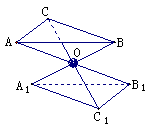 解:依题意,因为AA1、BB1、CC1相交于一点O,且
解:依题意,因为AA1、BB1、CC1相交于一点O,且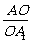 =
=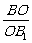 =
=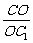 ,
,
所以AB∥A1B1,AC∥A1C1,BC∥B1C1
由平移角定理得
∠BAC=∠B1A1C1,∠ABC=∠A1B1C1,
△ ABC∽△A1B1C1,
△
所以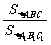 =(
=(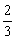 )2=
)2=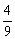
点评:利用平移定理,可证明空间两个角相等或两个三角形相似、全等;利用平行公理,可证明空间两条直线平行,从而解决相关问题
例5 ⑴已知水平平面 内的两条相交直线a, b所成的角为
内的两条相交直线a, b所成的角为 ,如果将角
,如果将角 的平分线
的平分线 绕着其顶点,在竖直平面内作上下转动, 转动到离开水平位值的
绕着其顶点,在竖直平面内作上下转动, 转动到离开水平位值的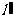 处,且与两条直线a,b都成角
处,且与两条直线a,b都成角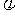 ,则
,则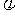 与
与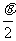 的大小关系是( )
的大小关系是( )
A 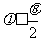 或
或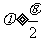 B
B 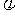 >
>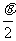 或
或 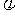 <
<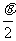 C
C 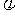 >
>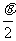 D
D 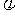 <
<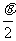
⑵已知异面直线a,b所成的角为70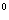 ,则过空间一定点O,与两条异面直线a,b都成60
,则过空间一定点O,与两条异面直线a,b都成60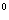 角的直线有 ( )
角的直线有 ( )
A 1条 B 2条 C 3条 D 4条
⑶异面直线a,b所成的角为 ,空间中有一定点O,过点O有3条直线与a,b所成角都是60°,则
,空间中有一定点O,过点O有3条直线与a,b所成角都是60°,则 的取值可能是( )
的取值可能是( )
A 30° B 50° C 60° D 90°
⑷一个凸多面体有8个顶点,①如果它是棱锥,那么它有 条棱, 个面;②如果它是棱柱,那么它有 条棱 个面
分析与解答:
⑴ 如图所示,
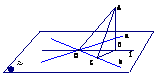
易知直线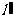 上点A在平面
上点A在平面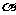 上的射影是点B,过点B作BC⊥b,
上的射影是点B,过点B作BC⊥b,
则AC⊥b 在Rt△OBC和Rt△OAC中,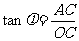 ,
,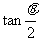 =
=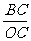 显然,AC>BC,
显然,AC>BC,
∴tan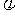 >
tan
>
tan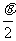 ,又
,又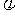 、
、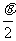
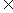 (0,
(0,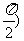 ,∴
,∴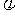 >
>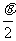 故选C
故选C
⑵如图所示,

过空间一点O分别作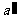 ∥a,
∥a,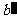 ∥b, 则
∥b, 则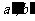 构成角
构成角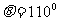 或 70
或 70
所求直线即为过点O且与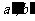 都成60
都成60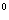 角的直线
角的直线
当 =110
=110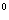 ,∴
,∴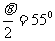 ,∴将两对对顶角的平分线绕O点分别在竖直平面内转动,总能得到与
,∴将两对对顶角的平分线绕O点分别在竖直平面内转动,总能得到与 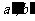 都60
都60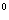 角的直线两条
角的直线两条
当 =70
=70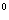 时,同理
时,同理
故 过点 O与a,b都成60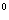 角的直线有4条,从而选 D
角的直线有4条,从而选 D
⑶过点O分别作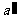 ∥a,
∥a,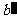 ∥b,则过点O有三条直线与
∥b,则过点O有三条直线与 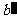
a,b所成角都为60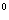 ,等价于过点O有三条直线与
,等价于过点O有三条直线与 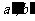 所成角都为60
所成角都为60 ,
,
如图所示,
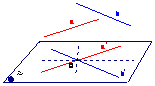
则 =60
=60 ,
,
 ,此时过点 O有三条直线与
,此时过点 O有三条直线与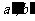 所成角都为60
所成角都为60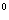 其中一条正是
其中一条正是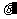 角的平分线
角的平分线
⑷①如果它是棱锥,则是七棱锥,有14条棱,8个面②如果它是棱柱,则是四棱柱,有12条棱,6个面
点评: 本题主要考查空间直线与直线、直线与平面、平面与平面间的位直关系,考查空间想象和转化能力,以及周密的分析问题和解决问题
小结:
1本节重点问题是证明三点共线、三线共点以及求异面直线所成的角
2证明三点均在两个平面的交线上,可以推证三点共线;求异面直线所成的角,一般先取一个特殊点作它们的平行线,作出所求的角或其补角,再解三角形
学生练习
1若a,b是异面直线,则只需具备的条件是
Aa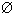 平面α,b
平面α,b 平面α,a与b不平行
平面α,a与b不平行
Ba 平面α,b
平面α,b 平面β,α∩β=l,a与b无公共点
平面β,α∩β=l,a与b无公共点
Ca∥直线c,b∩c=A,b与a不相交
Da⊥平面α,b 是α的一条斜线
答案:C
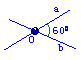 2如下图,直线a、b相交于点O且a、b成60°角,过点O与a、b都成60°角的直线有
2如下图,直线a、b相交于点O且a、b成60°角,过点O与a、b都成60°角的直线有
A1条 B2条 C3条 D4条
解析:在a、b所确定的平面内有一条,平面外有两条
答案:C
3如下图,正四面体S-ABC中,D为SC的中点,则BD与SA所成角的余弦值是
A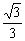 B
B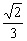 C
C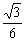 D
D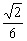
解析:取AC的中点E,连结DE、BE,则DE∥SA,
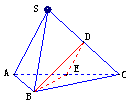 ∴∠BDE就是BD与SA所成的角设SA=a,
∴∠BDE就是BD与SA所成的角设SA=a,
则BD=BE=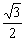 a,DE=
a,DE=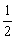 a,
a,
cos∠BDE=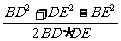 =
=
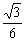
答案:C
4正方体ABCD-A1B1C1D1的棱长为a, 那么
(1)哪些棱所在直线与直线BA1成异面直线:__________
(2)直线BA1与CC1所成角的大小为________
(3)直线BA1与B1C所成角的大小为________
(4)异面直线BC与AA1的距离为________
(5)异面直线BA1与CC1的距离是________
答案:(1)D1C1、D1D、C1C、C1B1、DC、AD
(2)45° (3)60° (4)a (5)a
5正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,侧棱长为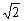 ,则这个棱柱的侧面对角线E1D与BC1所成的角是__________
,则这个棱柱的侧面对角线E1D与BC1所成的角是__________
解析:连结FE1、FD,则由正六棱柱相关性质可得FE1∥BC1,
在△EFD中,EF=ED=1,∠FED=120°,
∴FD=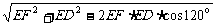 =
=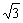
在△EFE1和△EE1D中,易得E1F=E1D=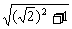 =
=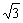 ,
,
∴△E1FD是等边三角形,∠FE1D=60°
而∠FE1D即为E1D与BC1所成的角
答案:60°
6两条相交直线l、m都在平面α内且都不在平面β内命题甲:l和m中至少有一条与β相交,命题乙:平面α与β相交,则甲是乙的
A充分不必要条件 B必要不充分条件
C充要条件 D非充分非必要条件
解析:若l和m中至少有一条与β相交,不妨设l∩β=A,则由于l α,∴A∈α而A∈β,∴α与β相交反之,若α∩β=a,如果l和m都不与β相交,由于它们都不在平面β内,
α,∴A∈α而A∈β,∴α与β相交反之,若α∩β=a,如果l和m都不与β相交,由于它们都不在平面β内,
∴l∥β且m∥β∴l∥a且m∥a,进而得到l∥m,与已知l、m是相交直线矛盾因此l和m中至少有一条与β相交
答案:C
7在棱长为2的正方体ABCD-A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点,那么异面直线OE和FD1所成的角的余弦值等于( )
A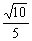 B
B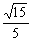 C
C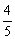 D
D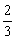
解法一:取面CC1D1D的中心为H,连结FH、D1H在△FHD1中,
FD1=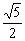 ,FH=
,FH=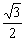 ,D1H=
,D1H=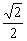
由余弦定理,得∠D1FH的余弦值为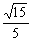
解法二:取BC的中点G连结GC1∥FD1,再取GC的中点H,连结HE、OH,则∠OEH为异面直线所成的角
在△OEH中,OE=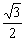 ,HE=
,HE=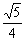 ,OH=
,OH=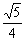
由余弦定理,可得cos∠OEH=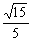
答案:B
8四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=2,EF⊥AB,则EF与CD所成的角等于___________
解析:取AD的中点G,连结EG、FG,易知EG=1,FG=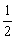
由EF⊥AB及GF∥AB知EF⊥FG
在Rt△EFG中,求得∠GEF=30°,即为EF与CD所成的角
答案:30°
9在正四棱锥P-ABCD中,若侧面与底面所成二面角的大小为60°,则异面直线PA与BC所成角的大小等于_______(结果用反三角函数值表示)
答案:arctan2
10设不全等的△ABC与△A1B1C1不在同一平面内,且AB∥A1B1,BC∥B1C1,CA∥C1A1
求证:AA1、BB1、CC1三线共点
证明:不妨设AB≠A1B1,AA1∩BB1=S,∵BC∥B1C1,∴BB1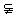 面BCC1B1,S∈面BBC1B1同理,S∈面ACC1A1∴S∈CC1,即AA1、BB1、CC1三线共点于S
面BCC1B1,S∈面BBC1B1同理,S∈面ACC1A1∴S∈CC1,即AA1、BB1、CC1三线共点于S
11在三棱锥A-BCD中,AD=BC=2a,E、F分别是AB、CD的中点,EF=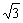 a,求AD与BC所成的角
a,求AD与BC所成的角
解:取AC的中点M,连结ME、MF,则ME∥BC,MF∥AD,所以∠EMF(或其补角)是直线AD与BC所成的角在△EMF中,ME=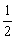 BC=a,MF=
BC=a,MF=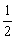 AD=a,EF=
AD=a,EF=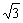 a,cos∠EMF=
a,cos∠EMF=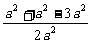 =-
=-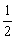 ,∠EMF=120°,因此异面直线AD与BC所成的角为60°
,∠EMF=120°,因此异面直线AD与BC所成的角为60°
12在三棱锥P-ABC中,AB=AC,PB=PC,E、F分别是PC和AB上的点且PE∶EC=AF∶FB=3∶2
(1)求证:PA⊥BC;
(2)设EF与PA、BC所成的角分别为α、β,求证:α+β=90°
证明:(1)取BC的中点D,连结AD、PD
则BC⊥平面ADP,AP 平面ADP,∴AP⊥BC
平面ADP,∴AP⊥BC
(2)在AC上取点G,使AG∶GC=3∶2,连结EG、FG,则EG∥PA,FG∥BC,从而∠EGF为PA与BC所成的角,由(1)知∠EGF=90°,
而∠GEF、∠GFE分别是EF与PA、EF与BC所成的角α、β,
∴α+β=90°
13如下图,已知空间四边形ABCD的对角线AC=10,BD=6,M、N分别是AB、CD的中点,MN=7,求异面直线AC与BD所成的角
解:取BC的中点E,连结EN、EM,
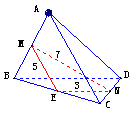 ∴∠MEN是异面直线AC与BD所成的角或其补角
∴∠MEN是异面直线AC与BD所成的角或其补角
在△EMN中,EN=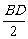 =3,EM=
=3,EM=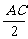 =5,MN=7,cos∠MEN=-
=5,MN=7,cos∠MEN=-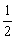 ,∴∠MEN=120°
,∴∠MEN=120°
∴异面直线AC与BD所成的角是60°
课前后备注
8.异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线 垂直,记作
垂直,记作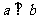 .
.
7.异面直线所成的角:已知两条异面直线 ,经过空间任一点
,经过空间任一点 作直线
作直线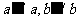 ,
, 所成的角的大小与点
所成的角的大小与点 的选择无关,把
的选择无关,把 所成的锐角(或直角)叫异面直线
所成的锐角(或直角)叫异面直线 所成的角(或夹角).为了简便,点
所成的角(或夹角).为了简便,点 通常取在异面直线的一条上
通常取在异面直线的一条上
异面直线所成的角的范围: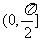
6.异面直线定理:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线
推理模式: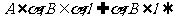
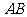 与
与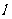 是异面直线
是异面直线
随着社会的发展,事物的变更,网络时代的迅速到来,很多新词语应运而生。如:偶、山寨、菜鸟、果酱、稀饭、恐龙、晒工资、白骨精、骨灰级、宅男宅女、人肉搜索、嘻哈文化等等。这些词语有的是旧词新解,有的纯属新兴词汇。
对此现象,舆论莫衷一是。有人认为新词语不仅丰富了语言,也记录着社会生活的巨大变革;有人认为这是语言发展的悲哀,丑陋恶俗的语言多起来,势必给灿烂的汉语言留下“黑点”;还有人认为……
你是怎样看待这一现象的?请结合自己的体验与积累写一篇文章。可以写自己的经历、感受和见解,可以讲述身边的故事,也可以发表评论。
[注意]①角度自选,立意自定,题目自拟。②除诗歌外,文体不限。③不少于800字。④不得抄袭。
 瑞安中学2007年级高三第一学期10月份考试
瑞安中学2007年级高三第一学期10月份考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com