
解:由题设: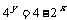 , 代入
, 代入 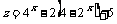
整理得: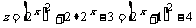
又∵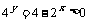 ,
∴
,
∴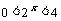
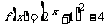 在
在 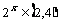 时是增函数
时是增函数
∴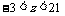
求:1°函数的定义域、值域 2°判断函数的奇偶性
解:1° 定义域为 R
由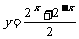 得
得 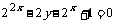
∵xÎR, ∴△≥0, 即  , ∴
, ∴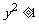 , 又∵
, 又∵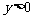 ,∴
,∴
2° ∵定义域为 R (是关于原点的对称区间)
又∵ 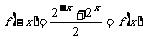 ,
∴
,
∴ 是偶函数。
是偶函数。
时,是增函数还是减函数?并证明之。
解:是减函数。
设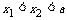 则
则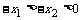
∵ 是偶函数, ∴
是偶函数, ∴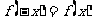 ∴
∴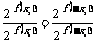
∵ 在 x>0, 时是增函数,且
在 x>0, 时是增函数,且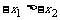 , ∴
, ∴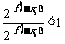
即 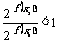 , 又:
, 又: ,
, 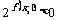 ∴
∴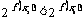 ,
,
∴ x<0 时,y是减函数。
2.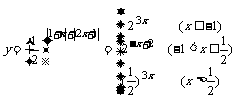
∴增区间为  减区间为
减区间为 
1.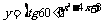 2.
2.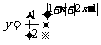
解:1.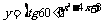
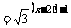
∴增区间为 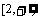 减区间为
减区间为 
解: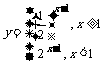
定义域:xÎR
值域: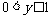
(其对称性与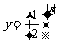 比较)
比较)
性质:定义域、值域、单调性、奇偶性 (略)
直线和平面平行的性质定理:
如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.
性质定理的证明:
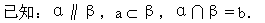
求证:a∥b.
例:
有一块木料,已知棱BC平行于面A′C′,要经过木料表面A′B′C′D′内的一点P和棱BC将木料锯开,应怎样画线?所画的线和面AC有什么关系?
练习:
在例中,若AD∥BC,BC∥面A′C′,那么,AD和面BC′、面BF、面A′C′都有怎样的位置关系,为什么?
P.22-23中习题三5、6、7、8.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com