
8.已知正项数列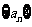 ,其前
,其前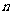 项和
项和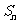 满足
满足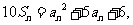 且
且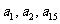 成等比数列,求数列
成等比数列,求数列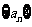 的通项
的通项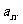
7. (1)数列{an}的前n项和为Sn,且a1=1,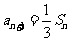 ,n=1,2,3,……,求
,n=1,2,3,……,求
数列{an}的通项公式;
(2) 数列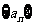 中,各项均为正数,且
中,各项均为正数,且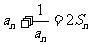 .求
.求
.
6. (1)数列{an}的前n项和Sn=3n-c, 则c=1是数列{an}为等比数列的 ( )
A 充分非必要条件 B 必要非充分条件 C充分必要条件 D 既非充分又非必要条件
(2)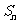 是数列
是数列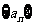 的前n项之和,而
的前n项之和,而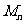 是数列
是数列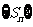 的前n项之和,且
的前n项之和,且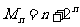 .求
.求
.
5.(1)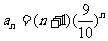 ,判断数列
,判断数列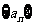 的单调性,并求数列
的单调性,并求数列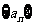 中的最大项.
中的最大项.
(2)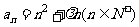 ,若
,若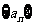 为单调递增的数列,求实数
为单调递增的数列,求实数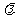 的取值范围.
的取值范围.
(3) 已知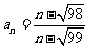
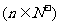 ,求数列
,求数列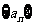 中的最大项和最小项.
中的最大项和最小项.
4. 已知数列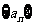 满足:
满足: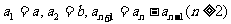 ,则
,则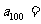 _____ ,
_____ ,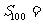 _____
_____
3.已知数列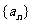 满足
满足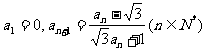 ,则
,则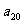 =( )
=( )
A.0 B.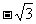 C.
C.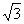 D.
D.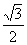
2.已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中=1,2,3,…
(1)证明数列{lg(1+an)}是等比数列;
(2)求数列{an}的通项;
1。(1)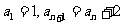 ,则
,则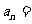 _________; 若
_________; 若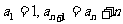 ,则
,则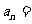 _________ .
_________ .
(2)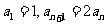 ,则
,则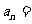 _________;若
_________;若 ,则
,则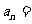 _________;
_________;
(3)已知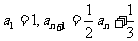 ,求
,求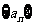 的通项公式______________
的通项公式______________
(4) 已知数列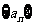 满足
满足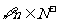 ,有
,有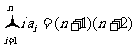 ,则
,则 =______________.
=______________.
(5) 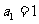 且对任意的
且对任意的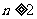 有
有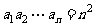 ,则数列的通项为__________
,则数列的通项为__________
(6)设{an}是首项是1的正项数列, 且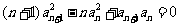 0(n=1.2,3,…),
0(n=1.2,3,…),
它的通项公式 = ______________.
= ______________.
1. 数列的基本问题及求解方法:
(1)求数列的通项公式: 观察,叠加,叠乘,数学归纳法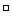 ,构造新的等差等比数列。
,构造新的等差等比数列。
(2)求数列的求和公式: 倒序相加,错位相减,裂项相消,公式,以及配对,分解通项公式.
(3)求数列的最大项: 判断数列的单调性(作差、商法),利用函数的单调性。
(4)任意 数列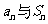 的关系是:_______________________________ .
的关系是:_______________________________ .
(5)数列的周期性:若存在常数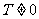 ,使
,使 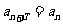 恒成立,则称
恒成立,则称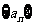 为周期数列.
为周期数列.
例题:
2.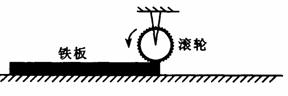 [苏北十校]16.(16分)如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放人工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
[苏北十校]16.(16分)如图所示,用半径为0.4m的电动滚轮在长薄铁板上表面压轧一道浅槽.薄铁板的长为2.8m、质量为10kg.已知滚轮与铁板、铁板与工作台面间的动摩擦因数分别为0.3和0.1.铁板从一端放人工作台的滚轮下,工作时滚轮对铁板产生恒定的竖直向下的压力为100N,在滚轮的摩擦作用下铁板由静止向前运动并被压轧出一浅槽.已知滚轮转动的角速度恒为5rad/s,g取10m/s2.
(1)通过分析计算,说明铁板将如何运动?
(2)加工一块铁板需要多少时间?
(3)加工一块铁板电动机要消耗多少电能?(不考虑电动机自身的能耗)
[解]16.解:(1)开始砂轮给铁板向前的滑动摩擦力F1=μ1FlN=0.3X100N=30N.
工作台给平板的摩擦阻力F2=μ2F2N=0.1X(100+l0X10)N=20N.
铁板先向右做匀加速直线运动a=(F1-F2)/m=1m/s2
加速过程铁板达到的最大速度vm=ωR=5X0.4m/s=2m/s.
这一过程铁板的位移Sl=vm/2a=2m<2.8m
此后砂轮给铁板的摩擦力将变为静摩擦力Fl,,Fl’=F2,铁板将做匀速运动.
即整个过程中铁板将先做加速度a=lm/s2的匀加速运动,然后做vm=2m/s的匀速运动(只要上面已求出,不说数据也得分)(7分)
(2)在加速运动过程中,由vm=at1得t1=2s,
匀速运动过程的位移为s2=L-s1=0.8m由s2=vt2,得t2=0.4s.
所以加工一块铁板所用的时间为T=t1+t2=2.4s.(4分)
(3)E=ΔEk+Q1+Q2=136J.(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com