
5. 曲线y=  在点(1,-1)处的切线方程为
在点(1,-1)处的切线方程为
(A)y=x-2
(B) y=-3x+2 (C)y=2x-3
(D)y=-2x+1

4. 已知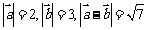 ,则
,则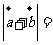 ( )
( )

A 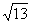 B.
B. 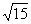 C
C
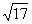 D
D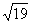

3.
已知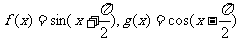 ,则下列结论中正确的是 ( )
,则下列结论中正确的是 ( )
A.函数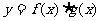 的周期为2
的周期为2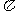 ;
;
B.函数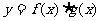 的最大值为1;
的最大值为1;
C.将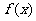 的图象向左平移
的图象向左平移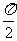 个单位后得到
个单位后得到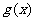 的图象;
的图象;
D.将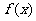 的图象向右平移
的图象向右平移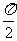 个单位后得到
个单位后得到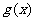 的图象;
的图象;
2. 已知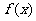 为偶函数,且
为偶函数,且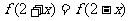 ,当
,当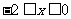 时
时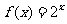 ,若
,若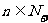 ,
,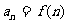 ,则
,则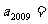 ( )
( )

A.2 B.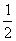 C.4 D.
C.4 D.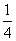

1.设集合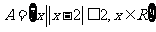 ,
,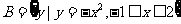 ,则
,则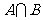 等于
等于
A.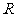 B.
B.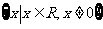 C.
C. D.
D.

18. [解析]
(1) f ’(x)=-3x2+6x+9 ........(2分)
令f ‘(x)<0,解得x<-1或x>3, ........(4分)
所以f(x)的递减区间为(-∞,-1)和(3,+∞) ........(6分)
(2)因为f(-2)=8+12-18+a =2+a ,f(2)=-8+12+18+a =22+a ,
所以f(2)>f(-2). ........(8分)
因为在(-1,3)上,f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,
于是有 22+a=20,解得 a=-2. ........(11分)
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,即函数f(x)在区间[-2,2] 


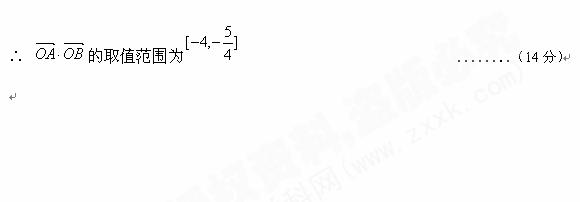
21.(本小题满分14分)已知平面上一定点C(-1,0)和一定直线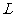 :
: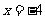 ,P为该平面上一动点,作
,P为该平面上一动点,作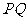 ⊥
⊥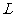 ,垂足为
,垂足为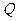 ,且
,且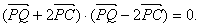

(1)求点P的轨迹方程;
(2)点O是坐标原点,过点C的直线与点P的轨迹交于A,B两点,求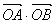 的取值范围.
的取值范围.
 又
又 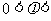
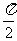 , ∴
, ∴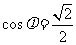 .......(13分)
.......(13分)
20.(本小题满分14分)若函数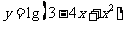 的定义域为M;当
的定义域为M;当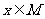 时,求
时,求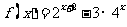 的最值及相应的x的值。
的最值及相应的x的值。






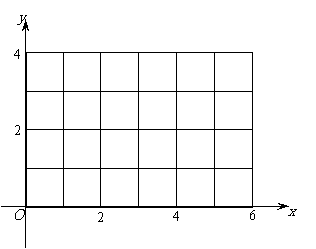
19.(本小题满分14分)某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件。
(1)设甲种设备需要生产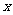 天, 乙种设备需要生产
天, 乙种设备需要生产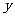 天, 该公司所需租赁费为
天, 该公司所需租赁费为 元,写出约束条件并画出平面区域;
元,写出约束条件并画出平面区域;
(2)求租赁费的最小值。




18. (本小题满分13分)已知函数
(本小题满分13分)已知函数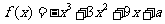

(1)求 的单调递减区间;
的单调递减区间;
(2)若 在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
在区间[-2,2]上的最大值为20,求它在该区间上的最小值.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com