
《课课练》 P75 例1.2
课时练习 4.5.6.7.8
补充:1.作下列函数图象:
1° 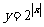 2°
2°  3°
3°
 4°
4°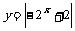
2.已知函数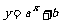 的图象过点(0,2)、(-2,11),求f(x).
的图象过点(0,2)、(-2,11),求f(x).
4.若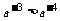 ,求a的取值范围。
,求a的取值范围。
解: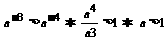
或解:由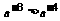 ∵
∵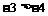 ∴
∴ 为增函数 ∴
为增函数 ∴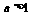
例三 求函数 的单调区间,并证明之。
的单调区间,并证明之。
解:设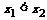 则
则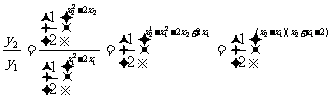
∵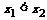 ∴
∴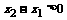
当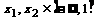 时,
时,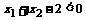 这时
这时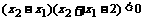
即 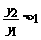 ∴
∴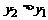 ,函数单调递增
,函数单调递增
当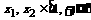 时,
时,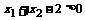 这时
这时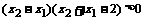
即  ∴
∴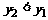 ,函数单调递减
,函数单调递减
∴函数y在 上单调递增,在
上单调递增,在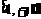 上单调递减。
上单调递减。
例四 证明函数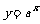 和
和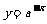
 的图象关于y轴对称。
的图象关于y轴对称。
证:设P1(x1,
y 1)是函数
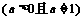 的图象上任意一点
的图象上任意一点
则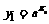 而P1(x1, y 1)关于y轴的对称点Q是(-x1, y 1)
而P1(x1, y 1)关于y轴的对称点Q是(-x1, y 1)
∴
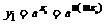 即Q在函数
即Q在函数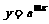 的图象上
的图象上
由于P1是任意取的
所以 上任一点关于y轴的对称点都在
上任一点关于y轴的对称点都在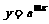 的图象上
的图象上
同理可证: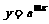 图象上任意一点也一定在函数
图象上任意一点也一定在函数 的图象上
的图象上
∴ 函数 和
和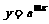 的图象关于y轴对称。
的图象关于y轴对称。
3. 和
和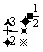 ∵
∵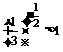
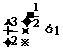 ∴
∴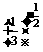 >
>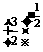
注意讲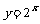 与
与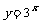 ,
, 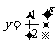 与
与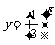 图象关系并推广
图象关系并推广
2. 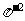 和
和 ∵指数
∵指数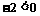 底数
底数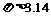 ∴
∴ <
<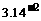
1.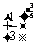 和
和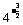 ∵
∵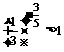
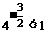 ∴
∴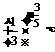
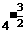
1.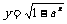 2.
2.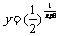
解:1.要使函数有意义,必须 2.要使函数有意义,必须
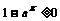
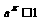
 即
即 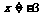
当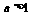 时
时  ∵
∵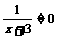
当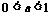 时
时  ∴
∴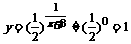
∵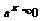 ∴
∴ 又∵
又∵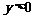
∴值域为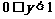 ∴值域为
∴值域为 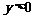 且
且
例二 比较下列两个值的大小:
2.根据判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行.
直线和平面的位置关系:
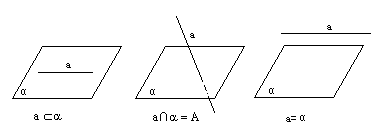
直线和平面平行的判定定理
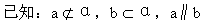
求证:a∥α
例:
已知:空间四边形ABCD中,E、F分别是AB、AD的中点.
求证:EF∥平面BCD.
1.根据定义:一般用反证法.
直线在平面外

P.22中习题三1、2、3、4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com