

20. (本小题满分14分)
已知函数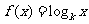 (
(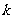 为常数,
为常数,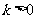 且
且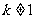 ),且数列
),且数列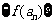 是首项为4,
是首项为4,
公差为2的等差数列.
(Ⅰ)求证:数列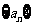 是等比数列;
是等比数列;
(Ⅱ) 若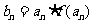 ,当
,当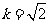 时,求数列
时,求数列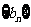 的前
的前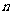 项和
项和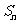 ;
;
(III)若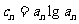 ,且
,且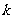 >1,比较
>1,比较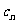 与
与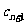 的大小.
的大小.
18. (本小题满分13分)
已知椭圆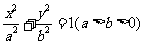 的左焦点为
的左焦点为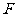 ,左右顶点分别为
,左右顶点分别为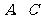 ,上顶点为
,上顶点为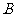 ,过
,过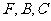 三点作圆
三点作圆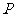 ,其中圆心
,其中圆心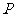 的坐标为
的坐标为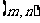 .
.
(Ⅰ)当 时,椭圆的离心率的取值范围.
时,椭圆的离心率的取值范围.
(Ⅱ)直线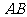 能否和圆
能否和圆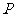 相切?证明你的结论.
相切?证明你的结论.
|
|
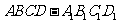 中,
中,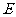 、
、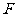 分
分
别为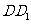 、
、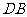 的中点.
的中点.
(Ⅰ)求证: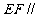 平面
平面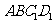 ;
;
(Ⅱ)求证: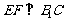 ;
;
(III)求三棱锥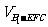 的体积.
的体积.
17. (本小题满分12分)
同时掷两个骰子,计算:
(Ⅰ)一共有多少种不同的结果?
(Ⅱ)其中向上的点数之和是5的结果有多少种?概率是多少?
(III)向上的点数之和小于5的概率是多少?
16.(本小题满分13分)
已知在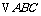 中,
中, 所对的边分别为
所对的边分别为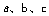 ,若
,若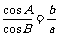 且
且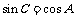
(Ⅰ)求角A、B、C的大小;
(Ⅱ)设函数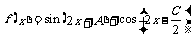 ,求函数
,求函数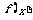 的单调递增区间,并指出它相邻两对称轴间的距离.
的单调递增区间,并指出它相邻两对称轴间的距离.
(二)选做题(14-15题,考生只能从中选做两题)
14.(坐标系与参数方程选做题)在极坐标系中,从极点O作直线与另一直线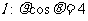 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使 .设R为
.设R为 上任意一点,则RP的最小值 .
上任意一点,则RP的最小值 .
15. (几何证明选讲选做题)如图,⊙O1与⊙O2交于M、N两
点,直线AE与这两个圆及MN依次交于A、B、C、D、E.且 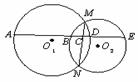
AD=19,BE=16,BC=4,则AE= .
|
11.右图是2008年北京奥运会上,七位评委为某奥运项目打出
的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩
数据的平均数为 ;方差为 .
12.在如下程序框图中,已知: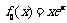 ,则输出的是_________ _.
,则输出的是_________ _.


13. 定义“等积数列”:在一个数列中,如果每一个项与它的后一项的积都为同一个常数,那末这个数列叫做等积数列,这个常数叫做该数列的公积。已知数列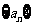 是等积数列,且
是等积数列,且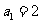 ,公积为5,
,公积为5,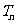 为数列
为数列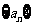 前
前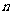 项的积,则
项的积,则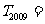
10.关于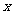 的方程
的方程 的两实根为
的两实根为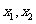 ,若
,若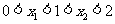 ,则
,则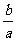 的取值范围是( )
的取值范围是( )
A.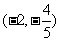 B.
B.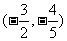 C.
C.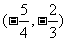 D.
D.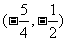
第Ⅱ卷(非选择题)
9.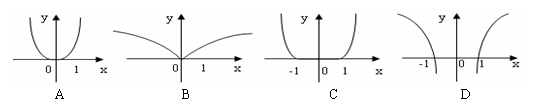 已知对数函数
已知对数函数 是增函数,则函数
是增函数,则函数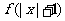 的图象大致是( )
的图象大致是( )
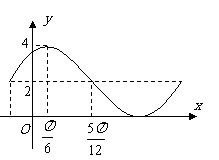
8.已知函数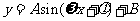 的一部分图象如图所示,
的一部分图象如图所示,
如果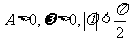 ,则(
)
,则(
)
A. B.
B.  C.
C.  D.
D.
7. 在平行四边形ABCD中,
在平行四边形ABCD中,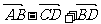 等于( )
等于( )
A.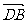 B.
B.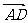 C.
C.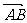 D.
D.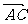
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com