
1. 下列情况中的加点物体,可以看作质点的是:
A.研究汽车后轮上一点运动情况的车轮
B.研究一列火车从北京开往上海所用的时间
C.体育教练员研究百米跑运动员的起跑动作
D.研究地球自转时的地球
21.[解析](Ⅰ)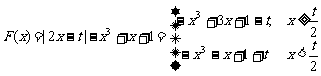
∴ 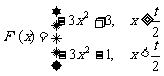 .……………..4分
.……………..4分
由-3x2+3=0 得x1=-1,x2=1,而-3x2-1<0恒成立,
∴ i) 当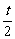 <-1时,F(x)在区间(-∞,-1)上是减函数,
<-1时,F(x)在区间(-∞,-1)上是减函数,
在区间(-1,1)上是增函数,在区间(1,+∞)上是减函数.
ii)
当1>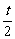 ≥-1时,F(x)在区间(-∞,
≥-1时,F(x)在区间(-∞,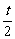 )上是减函数,
)上是减函数,
在区间(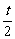 ,1)上是增函数,在区间(1,+∞)上是减函数.
,1)上是增函数,在区间(1,+∞)上是减函数.
iii)
当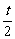 ≥1时,F(x)在(-∞,+∞)上是减函数. .……………..8分
≥1时,F(x)在(-∞,+∞)上是减函数. .……………..8分
(II)由1)可知
i) 当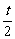 <-1时,F(x)在x=-1处取得极小值-1-t,
<-1时,F(x)在x=-1处取得极小值-1-t,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=-1-t或m=3-t.
ii)
当-1≤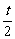 <1,F(x)在x=
<1,F(x)在x=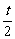 处取值为
处取值为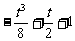 ,
,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=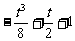 或m=3-t.
或m=3-t.
iii)
当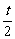 ≥1时,不存在这样的实数m,使得F(x)-m=0恰有两解..……………..14
≥1时,不存在这样的实数m,使得F(x)-m=0恰有两解..……………..14
[链接高考]本题是一道含参数的函数、导数与方程的综合题,需要对参数进行分类讨论. 在新高考中每年有一道导数综合题,同学们应高度重视.
20.[解析](Ⅰ) 证:由题意 ,即
,即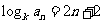 , ……2分
, ……2分
∴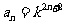 ∴
∴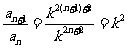 . ……4分
. ……4分
∵常数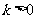 且
且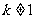 ,∴
,∴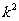 为非零常数,
为非零常数,
∴数列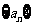 是以
是以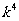 为首项,
为首项,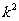 为公比的等比数列. ……6分
为公比的等比数列. ……6分
(II) 解:由(1)知,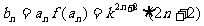 ,
,
当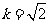 时,
时,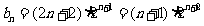 .
…………7分
.
…………7分
∴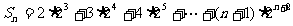 , ①
, ①
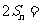
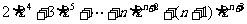 . ② ……9分
. ② ……9分
②-①,得
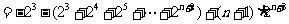
∴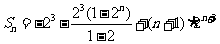
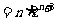 . ……11分
. ……11分
(III) 解:由(1)知,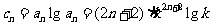 ;当
;当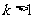 时,
时,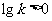 ,
,
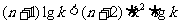 对一切
对一切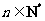 成立,即
成立,即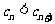 对一切
对一切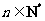 成立.…14分
成立.…14分
[链接高考]本题综合考查数列的基本知识、方法和运算能力,以及化归、转化的思想方法. 错位相减法是数列求和的一种重要方法,备考复习中要引起重视.
19.[解析](Ⅰ)连结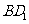 ,在
,在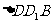 中,
中,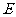 、
、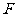 分别为
分别为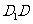 ,
,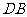 的中点,则
的中点,则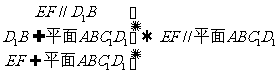 ………4分
………4分
(Ⅱ)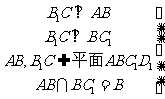

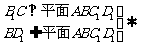
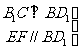
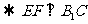 ……9分
……9分
(III) 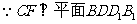
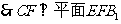 且
且  ,
,
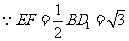 ,
,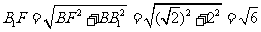 ,
,
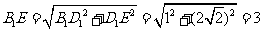 ∴
∴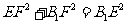 即
即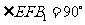 ;
;
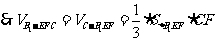 =
=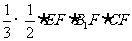 =
= .
.
……14分
[链接高考]本题主要考查线面平行、线面垂直、求锥体体积等立体几何知识,以及分析问题与解决问题的能力.
18. [解析](Ⅰ)由题意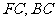 的中垂线方程分别为
的中垂线方程分别为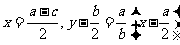 ,
,
于是圆心坐标为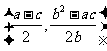 .
…………………………………4分
.
…………………………………4分
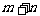 =
= ,即
,即 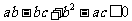 ,
,
即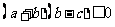 ,所以
,所以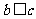 ,于是
,于是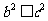 >
>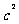 即
即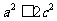 ,
,
所以 ,即
,即 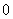 <
<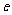 <
<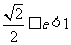 .
………………7分
.
………………7分
(Ⅱ)假设相切, 则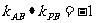 , ………………………………………9分
, ………………………………………9分
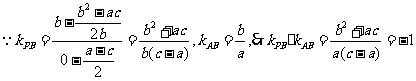 ,……11分
,……11分
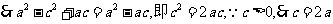 这与
这与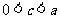 矛盾.
矛盾.
故直线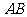 不能与圆
不能与圆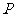 相切. ………………………………………………13分
相切. ………………………………………………13分
[链接高考] 本题主要考查直线与圆、椭圆的位置关系以及分析问题与解决问题的能力.圆锥曲线与圆的综合题经常出现在高考试题中,要引起足够的重视.
17.[解析](Ⅰ)掷一个骰子的结果有6种.
我们把两个骰子标上记号1,2以便区分,由于1号骰子的每一个结果都可以与2号骰子的任意一个结果配对,组成同时掷两个骰子的结果,因此同时掷两个骰子的结果共36种.
……3分
(Ⅱ)在上面的所有结果中,向上的点数之和为5的结果有(1,4),(2,3),(3,2),(4,1)共4种.
由于所有36种结果是等可能的,其中向上的点数之和为5的结果有4种,因此由古典概型的概率计算公式可得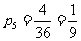 ……7分
……7分
(III)向上的点数之和为2的结果有(1,1)一种情况,向上的点数之和为3的结果有(1,2),(2,1)两种情况,向上的点数之和为4的结果有(1,3),(3,1),(2,2)三种情况。
记向上的点数之和为2的概率为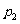 ,向上的点数之和为3的概率为
,向上的点数之和为3的概率为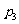 ,向上的点数之和为4的概率为
,向上的点数之和为4的概率为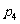 ,因此,向上的点数之和小于5的概率
,因此,向上的点数之和小于5的概率
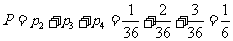 ……12分
……12分
[链接高考]概率与统计的综合题,自从2005年走进新高考试题中,就以崭新的姿态,在高考中占有极其重要的地位,每年出现一道大题,必须充分重视.要提高此类解答题的得分,在解答时,一定要详细地写出过程.
16.[解析](Ⅰ)由题设及正弦定理知: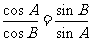 ,得
,得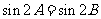
∴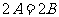 或
或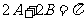 ,即
,即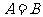 或
或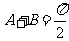
当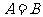 时,有
时,有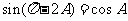 , 即
, 即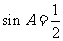 ,得
,得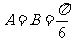 ,
,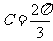 ;
;
当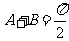 时,有
时,有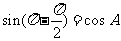 ,即
,即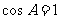 不符题设
不符题设
∴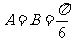 ,
,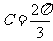 …………………7分
…………………7分
(Ⅱ) 由(Ⅰ)及题设知: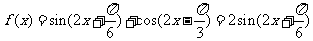
当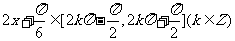 时,
时, 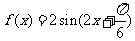 为增函数
为增函数
即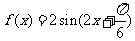 的单调递增区间为
的单调递增区间为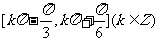 . ………12分
. ………12分
它的相邻两对称轴间的距离为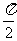 . ………13分
. ………13分
[链接高考] 解决本题的关键是,利用正弦定理把三角形边角问题转化为三角函数问题是解题的关键,三角形与三角函数、向量与三角函数高考考察的热点.
(二)选做题(13-15题,考生只能从中选做两题)
14.(坐标系与参数方程选做题)[解析]1.设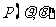 ,
,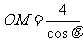 ,
,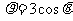 .故P在圆:
.故P在圆: 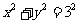 上,而R为直线
上,而R为直线 :
: 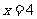 .由图象知,
.由图象知,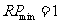 .
.
[链接高考]本小题主要考查直线与圆的极坐标方程的有关知识,以及转化与化归的思想方法.解决本题的关键是将它们转化为直角坐标系下的直线与圆的位置关系问题来处理.
15. (几何证明选讲选做题)[解析]28.因为A,M,D,N四点共圆,所以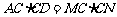 .同理,有
.同理,有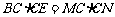 .所以
.所以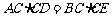 ,即
,即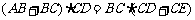 ,所以 AB·CD=BC·DE.
,所以 AB·CD=BC·DE.
设CD=x,则AB=AD- BC-CD=19-4-x=15-x, DE=BE- BC-CD=16-4-x=12-x,则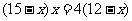 ,即
,即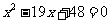 ,解得
,解得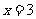 或
或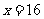 (舍).
(舍).
AE=AB+ DE- BD=19+16-7=28.
[链接高考]本小题主要考查两圆的位置关系,以及相交弦定理的有关知识,分析问题和解决问题的能力,以及转化与化归的思想方法.
10.[解析]D.设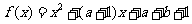 ,则方程
,则方程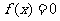 的两实根
的两实根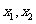 满足
满足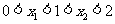 的
的
充要条件是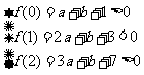 ,作出点
,作出点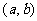 满足的可行域为Δ
满足的可行域为Δ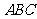 的内部,其中点
的内部,其中点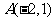 、
、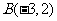 、
、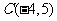 ,
,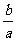 的几何意义是Δ
的几何意义是Δ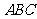 内部任一点
内部任一点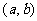 与原点
与原点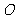 连线的斜率,而
连线的斜率,而 ,
, ,
,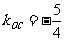 作图,易知
作图,易知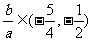 .
.
[链接高考]本小题是一道以二次方程的根的分布为载体的线性规划问题,考查化归转化和数形结合的思想,能力要求较高.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com