
函数 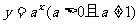 叫做指数函数,其中x是自变量,函数的定义域是R。
叫做指数函数,其中x是自变量,函数的定义域是R。
注意:为什么要规定 a>0且a¹1:∵a<0时 ax 不一定有意义
a=0时,若x>0,ax=0;若x<0,则ax无意义
a=1时,y=1x=1(常量)没有研究必要。
为了避免上述各种情况,所以规定a>0且a¹1。
4.在长方体ABCD-A1B1C1D1中,∠BAB1=∠B1A1C1=30°.求:(1)AB与A1C1所成的角的度数;(2)A1A与CB1所成的角的度数;(3)AB1与A1C1所成的角的余弦.
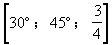
例1 在长方体ABCD-A1B1C1D1中,AB=BC=3,AA1=4.求异面直线A1B和AD1所成的角的余弦.(如图1)

师:首先我们要以概念为指导作出这个角,A1B和AD1所成的角是哪一个角?
生:因为CD1∥A1B,所以∠AD1C即为A1B与AD1所成的角.
师:∠AD1C在△AD1C中,求出△AD1C的三边,然后再用余弦定理求出∠AD1C的余弦.
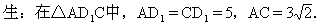
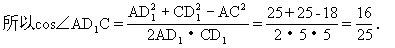
师:我们要再一次明确求异面直线所成的角的三个步骤:第一是以概念为指导作出所成的角;第二是找出这个角所在的三角形;第三是解这个三角形.现在我们再来看例2.
例2 在长方体ABCD-A1B1C1D1中,∠C1BC=45°,∠B1AB=60°.求AB1与BC1所成角的余弦.(如图2)
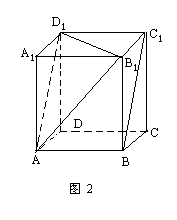
师:在这例中,我们除了首先要以概念为指导作出异面直线所成的角以外,还要注意把所给的特殊角的条件转化为长方体各棱之间的关系,以便于我们用余弦定理.
生:因为BC1∥AD1,所以AB1与BC1所成的角即为∠D1AB1.根
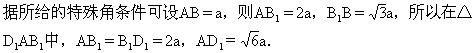
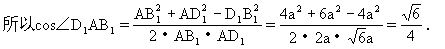
师:现在我们来看例3.
例3 已知正方体的棱长为a,M为AB的中点,N为B1B的中点.求A1M与C1N所成的角的余弦.(如图3)(1992年高考题)
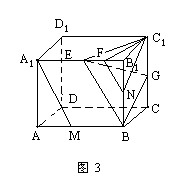
师:我们要求A1M与C1N所成的角,关键还是以概念为指导作出这个角,当一次平移不行时,可用两次平移的方法.在直观图中,根据条件我们如何把A1M用两次平移的方法作出与C1N所成的角?
生:取A1B1的中点E,连BE,由平面几何可知BE∥A1M1,再取EB1的中点F,连FN由平面几何可知FN∥BE,所以NF∥A1M.所以∠C1NF即为A1M与C1N所成的角.
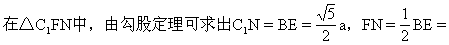
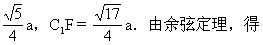
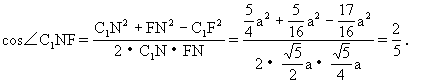
师:还可以用什么方法作出A1M与C1N所成的角?
生:当BE∥A1M后,可取C1C中点G,连BG,则BG∥C1N,

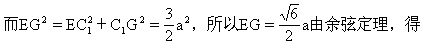
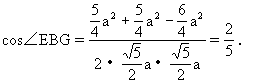
师:这两种解法都要用两次平移来作出异面直线所成的角,现在我们来看例4.
例4 在长方体ABCD-A1B1C1D1中,AA1=c,AB=a,AD=b,且a>b.求AC1与BD所成的角的余弦.(如图4)
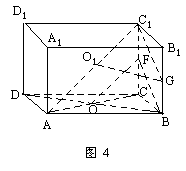
师:根据异面直线所成的角的概念,再根据长方体的基本性质,如何作出AC1与BD所成的角。
生:连AC,设AC∩BD=0,则O为AC中点,取C1C的中点F,

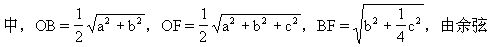
定理,得

师:想一想第二个解法
生:取AC1中点O1,B1B中点G.在△C1O1G中,∠C1O1G即
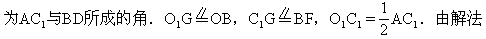
一可知:
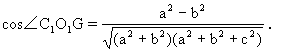
师:想一想第三个解法.当然还是根据异面直线所成的角概念首先作出这个角.有时可根据题目的要求在长方体外作平行直线.
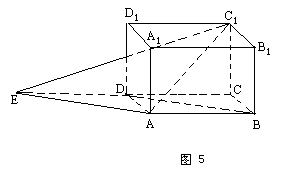
生:延长CD到E,使ED=DC.则ABDE为平行四边形.AE∥BD,所以∠EAC1即为AC1与BD所成的角.(如图5)连EC1,在
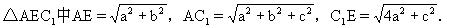
由余弦定理,得
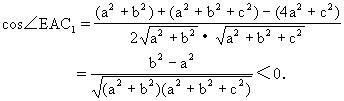
所以∠EAC1为钝角.
根据异面直线所成角的定义,AC1与BD所成的角的余弦为
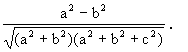
师:根据这一道题的三种解法,我们可以看出,当用异面直线所成的角的概念,作出所成的角,这时所作出的角可能是异面直线所成的角,也可能是它的邻补角,在直观图中无法判定,只有通过解三角形后,根据这个角的余弦的正、负值来判定这个角是锐角(也就是异面直线所成的角)或钝角.(异面直线所成的角的邻补角)
今天就讲这四个例题,这四个例题都是要用余弦定理来求异面直线所成的角.
作业
补充题
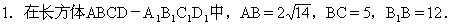

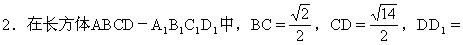

3.在棱长为a的正方体ABCD-A1B1C1D1中,O是正方形ABCD的中心,E,F分别是AB,BC中点.求:(1)异面直线A1D1和CD的距离;(2)异面直线C1O和EF的距离.
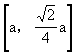
师:余弦定理有哪两种表述的形式?它们各有什么用途?
生:余弦定理有两种表述的形式,即:
a2=b2+c2-2bccos A
b2=c2+a2-2cacos B
c2=a2+b2-2abcos C

第一种形式是已知两边夹角用来求第三边,第二种形式是已知三边用来求角.
师:在立体几何中我们主要用余弦定理的第二种形式,即已知三角形的三边来求角.
在余弦定理的第二个形式中,我们知道b2+c2可以等于a2;也可以小于a2;也可以大于a2.那么,我们想当b2+c2=a2时,∠A等于多少度?为什么?
生:当b2+c2=a2时,由勾股定理的逆定理可知∠A=90°.
师:当b2+c2>a2时,∠A应该是什么样的角呢?
生:因为cosA>0,所以∠A应该是锐角.
师:当b2+c2<a2时,∠A应该是什么样的角呢?
生:因为这时cosA<0,所以∠A应该是钝角.
师:对,关于这个问题,我们只要求同学们有初步的理解即可.初步理解后应该记住、会用.现在明确提出当cosθ=0时,θ=90°,θ是直角;当cosθ>0时,0°<θ<90°,θ是锐角当cosθ<0时,90°<θ<180°,θ是钝角.下面请同学们回答下列问题:
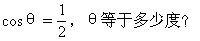
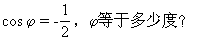
生:θ等于60°,
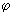 等于120°.
等于120°.
师:这时θ和 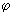 是什么关系?
是什么关系?
生:θ和 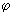 是互为补角.
是互为补角.
师:再回答下列问题:
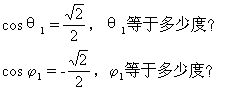
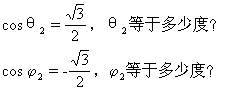
生:θ1等于45°,
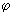 1等于135°,θ1+
1等于135°,θ1+ 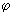 1=180°;θ2等于30°,
1=180°;θ2等于30°, 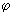 2=150°,θ2+
2=150°,θ2+ 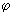 2=180°.
2=180°.
师:一般说来,当cosθ=-cos 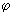 时,角θ与角
时,角θ与角
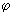 是什么关系?
是什么关系?
生:角θ与角 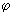 是互补的两个角.即一个为锐角,一个
是互补的两个角.即一个为锐角,一个
为钝角,且θ+ 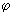 =180°.
=180°.
(关于钝角的三角函数还没有定义,所以这里采用从特殊到一般的方法使学生有所理解即可)
3.下列5个命题中正确的是
①对于实数p,q和向量 ,若p
,若p =q
=q 则p=q②对于向量
则p=q②对于向量 与
与 ,若|
,若| |
| =|
=| |
| 则
则 =
= ③对于两个单位向量
③对于两个单位向量 与
与 ,若|
,若| +
+ |=2则
|=2则 =
= ④对于两个单位向量
④对于两个单位向量 与
与 ,若k
,若k =
= ,则
,则 =
=
2.下列命题中,正确命题的个数为( A )
①若 与
与 是非零向量 ,且
是非零向量 ,且 与
与 共线时,则
共线时,则 与
与 必与
必与 或
或 中之一方向相同;②若
中之一方向相同;②若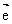 为单位向量,且
为单位向量,且 ∥
∥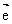 则
则 =|
=| |
|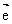 ③
③ ·
· ·
· =|
=| |
|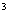 ④若
④若 与
与 共线,
共线, 与
与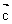 共线,则
共线,则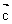 与
与 共线;⑤若平面内四点A.B.C.D,必有
共线;⑤若平面内四点A.B.C.D,必有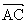 +
+ =
=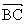 +
+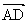
A 1 B 2 C 3 D 4
1.下面5个命题中正确的有( )
① =
=

 ·
·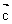 =
= ·
·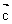 ; ②
; ② ·
·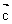 =
= ·
·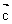

 =
= ;③
;③ ·(
·( +
+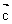 )=
)= ·
·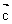 +
+ ·
·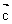 ;
;
④ ·(
·( ·
·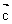 )=(
)=( ·
· )·
)·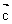 ; ⑤
; ⑤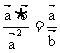 .
.
A..①②⑤ B.①③⑤ C. ②③④ D. ①③
例1.对于任意非零向量 与
与 ,求证:||
,求证:|| |-|
|-| ||≤|
||≤| ±
± |≤|
|≤| |+|
|+| |
|
证明:(1)两个非零向量 与
与 不共线时,
不共线时, +
+ 的方向与
的方向与 ,
, 的方向都不同,并且|
的方向都不同,并且| |-|
|-| |<|
|<| ±
± |<|
|<| |+|
|+| |
|
(3)两个非零向量 与
与 共线时,①
共线时,① 与
与 同向,则
同向,则 +
+ 的方向与
的方向与 .
. 相同且|
相同且| +
+ |=|
|=| |+|
|+| |.②
|.② 与
与 异向时,则
异向时,则 +
+ 的方向与模较大的向量方向相同,设|
的方向与模较大的向量方向相同,设| |>|
|>| |,则|
|,则| +
+ |=|
|=| |-|
|-| |.同理可证另一种情况也成立。
|.同理可证另一种情况也成立。
例2 已知O为△ABC内部一点,∠AOB=150°,∠BOC=90°,设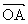 =
= ,
,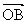 =
= ,
,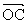 =
=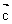 ,
,
且| |=2,|
|=2,| |=1,|
|=1,| 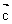 |=3,用
|=3,用 与
与 表示
表示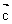

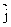
解:如图建立平面直角坐标系xoy,其中 ,
, 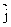 是单位正交基底向量, 则B(0,1),C(-3,0),设A(x,y),则条件知x=2cos(150°-90°),y=-2sin(150°-90°),即A(1,-
是单位正交基底向量, 则B(0,1),C(-3,0),设A(x,y),则条件知x=2cos(150°-90°),y=-2sin(150°-90°),即A(1,-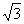 ),也就是
),也就是 =
= -
-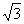
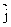 ,
,  =
=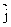 ,
, 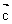 =-3
=-3 所以-3
所以-3 =3
=3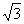
 +
+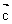 |即
|即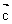 =3
=3 -3
-3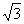

例3.下面5个命题:①| ·
· |=|
|=| |·|
|·| |②(
|②( ·
· )
)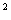 =
=
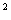 ·
·
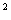 ③
③ ⊥(
⊥( -
-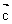 ),则
),则 ·
·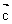 =
= ·
·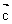 ④
④ ·
· =0,则|
=0,则| +
+ |=|
|=| -
- |⑤
|⑤ ·
· =0,则
=0,则 =
=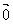 或
或 =
=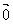 ,其中真命题是( )
,其中真命题是( )
A①②⑤ B ③④ C①③ D②④⑤
向量知识,向量观点在数学.物理等学科的很多分支有着广泛的应用,而它具有代数形式和几何形式的“双重身份”能融数形于一体,能与中学数学教学内容的许多主干知识综合,形成知识交汇点,所以高考中应引起足够的重视. 数量积的主要应用:①求模长;②求夹角;③判垂直
8. 数量积(点乘或内积)的概念, ·
· =|
=| ||
|| |cos
|cos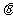 =x
=x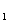 x
x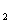 +y
+y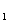 y
y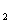 注意区别“实数与向量的乘法;向量与向量的乘法”
注意区别“实数与向量的乘法;向量与向量的乘法”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com